题目内容
若不等式 的解集为{x|-3≤x<-1,或x≥2},则a+m+n=( )
的解集为{x|-3≤x<-1,或x≥2},则a+m+n=( )A.-4
B.-6
C.0
D.5
【答案】分析:根据不等式的解集把原不等式转化为x+3,x-2与x+1相乘的形式,即可得到a的值,利用韦达定理即可求出m与n的值,求出a+m+n的值即可.
解答:解:由原不等式的解集为{x|-3≤x<-1,或x≥2},
则不等式可化为:(x2+mx+n)(x+a)≥0,
即(x+3)(x-2)(x+1)≥0,
得到:a=1,-m=-3+2即m=1,n=-3×2=-6,
则a+m+n=1+1+(-6)=-4.
故选A
点评:此题考查了其他不等式的解法,考查了转化的数学思想,要求学生灵活运用韦达定理化简求值,是一道基础题.
解答:解:由原不等式的解集为{x|-3≤x<-1,或x≥2},
则不等式可化为:(x2+mx+n)(x+a)≥0,
即(x+3)(x-2)(x+1)≥0,
得到:a=1,-m=-3+2即m=1,n=-3×2=-6,
则a+m+n=1+1+(-6)=-4.
故选A
点评:此题考查了其他不等式的解法,考查了转化的数学思想,要求学生灵活运用韦达定理化简求值,是一道基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
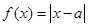 .
.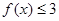 的解集为{x|-1≤x≤5},求实数a的值;
的解集为{x|-1≤x≤5},求实数a的值;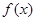 +
+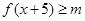 对一切实数x恒成立,求实数m的取值范围.
对一切实数x恒成立,求实数m的取值范围. 的解集为{x ︳-
的解集为{x ︳- <
x <
<
x < }
, 则 a + b 的值为
}
, 则 a + b 的值为 .
.