题目内容
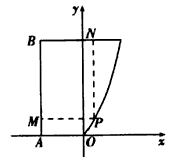
某地政府为科技兴市,欲将如图所示的一块不规则的非农业地规划建成一个矩形高科技工业园,已知AB⊥BC,OA∥BC,且|AB|=|BC|=4km.|AO|=2km,曲线段OC 是以点O为顶点且开口向上的一段抛物线,如果要使矩形的两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园的用地面积最大?并求出最大的用地面积(精确到0.1 km2)。
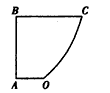
| 解:以O为原点,OA所在直线为x轴建立直角坐标系,如图所示, 依题意可设抛物线的方程为x2=2py(p >0),且过点C(2,4), 所以22=2p× 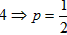 故曲线段OC的方程为y =x2(0≤x≤2), 设P(x,x2)(0≤x≤2)是曲线段OC上的任意一点, 则|PM|=2+x,|PN|=4-x2, 所以, 工业园的用地面积S=|PM|·|PN|=(2+x)(4- x2)=-x3-2x2+4x+8, 所以, S′=-3x2-4x+4, 令S′=0,得 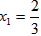 ,x2=-2, ,x2=-2,又因为0≤x≤2, 所以 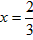 , ,当 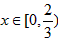 时,S′>0,S是x的增函数; 时,S′>0,S是x的增函数;当 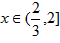 时,S′<0,S是x的减函数, 时,S′<0,S是x的减函数,所以,当 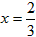 时,S取得最大值, 时,S取得最大值,此时 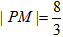 ·|PN|= ·|PN|=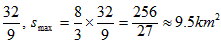 故把工业园规划成长为 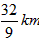 ,宽为 ,宽为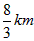 时,工业园的用地面积最大,约为9.5km2。 时,工业园的用地面积最大,约为9.5km2。 |
 |

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
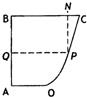 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA∥BC,且AB=BC=4km,AO=2km,曲线段OC是以点O为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2).
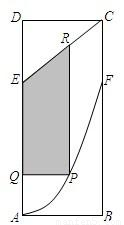
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA∥BC,且AB=BC=4km,AO=2km,曲线段OC是以点O为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上.问:应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2).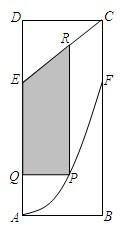 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.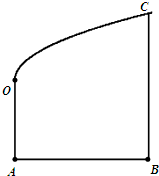 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知AB⊥BC,DA∥BC且AB=BC=2AD=4km,曲线段OC是以点O为顶点且开口向右的抛物线的一段.
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知AB⊥BC,DA∥BC且AB=BC=2AD=4km,曲线段OC是以点O为顶点且开口向右的抛物线的一段. 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km其中曲线段AF是以A为顶点、AD为对称轴的抛物线的一部分.分别以直线AB,AD为x轴和y轴建立平面直角坐标系.