题目内容
已知圆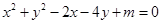 .(14分)
.(14分)
(1)此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且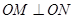 (O为坐标原点),求m的值;
(O为坐标原点),求m的值;
(3)在(2)的条件下,求以 为直径的圆的方程.
为直径的圆的方程.
【答案】
(1)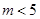 (2)
(2)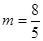 (3)
(3)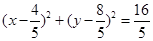
【解析】
试题分析:(1)把方程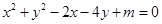 化为圆的标准方程为
化为圆的标准方程为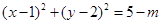 ,故有
,故有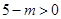 ,由此解得
,由此解得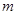 的范围.
的范围.
(2)由直线方程与圆的方程联立消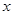 ,把直线
,把直线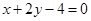 代入圆的方程化简到关于
代入圆的方程化简到关于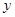 的二次方程,设
的二次方程,设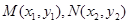 .∵
.∵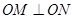 ,故
,故
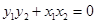 ①,利用根与系数的关系可得
①,利用根与系数的关系可得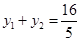 ,
,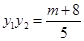 ,代入①求得
,代入①求得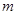 的值.
的值.
(3)由(2)可以求出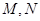 两点的坐标,由两点间距离公式可以求出线段
两点的坐标,由两点间距离公式可以求出线段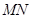 的长度,再由中点公式可以求出圆心.可以得到以
的长度,再由中点公式可以求出圆心.可以得到以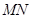 直径的圆的方程.当然也可以圆的直径式
直径的圆的方程.当然也可以圆的直径式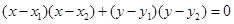 直接写出圆的方程.
直接写出圆的方程.
试题解析:
(1)方程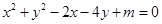 ,可化为
,可化为
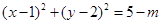 ,
,
∵此方程表示圆,
∴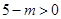 ,即
,即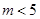 .
.
(2)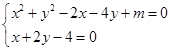
消去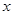 得
得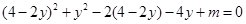 ,
,
化简得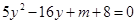 .
.
设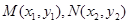 ,则
,则
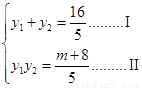
由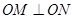 得
得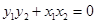
即 ,
,
∴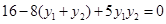 .
.
将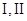 两式代入上式得
两式代入上式得
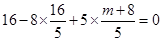 ,
,
解之得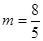 .
.
(3)由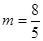 ,代入
,代入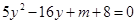 ,
,
化简整理得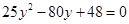 ,解得
,解得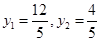 .
.
∴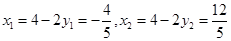 .
.
∴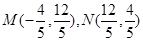 ,
,
∴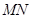 的中点C的坐标为
的中点C的坐标为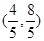 .
.
又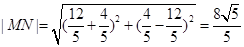 ,
,
∴所求圆的半径为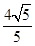 .
.
∴所求圆的方程为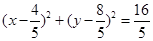 .
.
考点:圆的一般方程; 二元二次方程表示圆的条件;圆的标准方程;直线与圆的位置关系.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
 ,求直线l的方程;
,求直线l的方程; ,求动点Q的轨迹方程,并说明此轨迹是什么曲线。
,求动点Q的轨迹方程,并说明此轨迹是什么曲线。