题目内容
【题目】已知过抛物线y2=6x焦点的弦长为12,则该弦所在直线的倾斜角是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]()
【答案】B
【解析】
根据抛物线方程,求得焦点坐标为F(![]() ,0),从而设所求直线方程为y=k(x﹣
,0),从而设所求直线方程为y=k(x﹣![]() ).再将所得方程与抛物线y2=6x消去y,得k2x2﹣(3k2+6)x+
).再将所得方程与抛物线y2=6x消去y,得k2x2﹣(3k2+6)x+![]() k2=0,利用一元二次根与系数的关系,得x1+x2=
k2=0,利用一元二次根与系数的关系,得x1+x2=![]() ,最后结合直线过抛物线y2=6x焦点截得弦长为12,得到x1+x2+3=12,所以
,最后结合直线过抛物线y2=6x焦点截得弦长为12,得到x1+x2+3=12,所以![]() =9,解之得k2=1,得到直线的倾斜角.
=9,解之得k2=1,得到直线的倾斜角.
∵抛物线y2=6x,∴2p=6.∴![]() ,
,
即焦点坐标F![]() .
.
设所求直线方程为y=k![]() ,与抛物线y2=6x消去y,
,与抛物线y2=6x消去y,
得k2x2-(3k2+6)x+![]() k2=0.
k2=0.
设直线交抛物线于A(x1,y1),B(x2,y2),则x1+x2=![]() .
.
∵直线过抛物线y2=6x焦点,弦长为12,
∴x1+x2+3=12.∴x1+x2=9,即![]() =9,
=9,
解得k2=1,k=tan α=±1.
∵α∈[0,π),∴α=![]() 或
或![]() .
.
故选B

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】某房产中介统计了深圳市某高档小区从2018年12月至2019年11月当月在售二手房均价(单位:万元/平方米)的散点图,如下图所示,图中月份代码1至12分别对应2018年12月至2019年11月的相应月份.
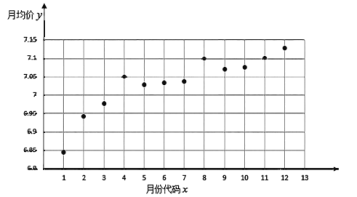
根据散点图选择![]() 和
和![]() 两个模型进行拟合,根据数据处理得到两个回归方程分别为
两个模型进行拟合,根据数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.0148557 | 0.0048781 |
总偏差平方和 | 0.069193 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2020年5月份购买深圳市福田区![]() 平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
平方米的二手房(欲购房为其家庭首套房).若该小区所有住房的房产证均已满3年,请你利用(1)中拟合效果更好的模型解决以下问题:
(i)估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.01万元/平方米)
(ii)若该购房者拟用不超过760万元的资金购买该小区一套二手房,试估算其可购买的最大面积(精确到1平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按照房屋的计税价格进行征收.(计税价格=房款)
征收方式见下表:
购买首套房面积 |
|
|
|
契税(买方缴纳)的税率 |
|
|
|
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关指数 .
.