题目内容
12.若函数f(x)=3sinx-4cosx,则f′($\frac{π}{2}$)=4.分析 根据求导法则,先求导,再代入值计算.
解答 解:∵f′(x)=3cosx+4sinx,
∴f′($\frac{π}{2}$)=3cos$\frac{π}{2}$+4sin$\frac{π}{2}$=4.
故答案为:4.
点评 本题考查了导数的运算法则,掌握求导公式是关键,属于基础题.

练习册系列答案
相关题目
2.已知函数y=$\left\{\begin{array}{l}{a{x}^{2},x≤0}\\{(a-4)x+a-3,x>0}\end{array}\right.$,是定义域上的减函数,则实数a的取值范围的( )
| A. | a>0 | B. | a<4 | C. | 0<a≤3 | D. | 3≤a<4 |
3.函数$f(x)={log_2}x+{2^x}$在闭区间[1,4]上的最小值与最大值分别为( )
| A. | -1,20 | B. | 2,18 | C. | 15,20 | D. | 16,18 |
20.已知 A(-2,3)、B(4,-3)两点,则线段AB的中点坐标是( )
| A. | (3,0) | B. | (2,3) | C. | (3,3) | D. | (1,0) |
17.如图是高中课程结构图:地理所属课程是( )
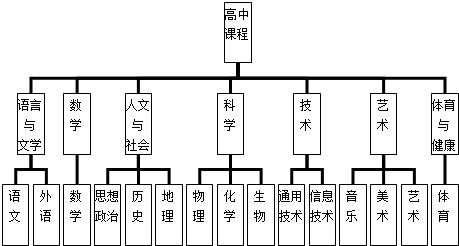

| A. | 人文与社会 | B. | 文科 | C. | 思想政治 | D. | 科学 |
1.下列函数中,为偶函数的是( )
| A. | y=x+1 | B. | y=$\frac{1}{x}$ | C. | y=x4 | D. | y=x5 |