题目内容
在三角形中有下面的性质:
(1)三角形的两边之和大于第三边;
(2)三角形的中位线等于第三边的一半;
(3)三角形的三条内角平分线交于一点,且这个点是三角形的内心;
(4)三角形的面积为S=
(a+b+c)r(r为三角形内切圆半径).
请类比出四面体的有关相似性质.
(1)三角形的两边之和大于第三边;
(2)三角形的中位线等于第三边的一半;
(3)三角形的三条内角平分线交于一点,且这个点是三角形的内心;
(4)三角形的面积为S=
| 1 | 2 |
请类比出四面体的有关相似性质.
分析:平面中边类比到空间的面,中位线类比到中位面(过棱的中点的面),平面中的长度类比到空间的面积,平分线类比到二面角的平分面,内心类比到内切球的球心,面积类比到体积,从而得到四面体的有关相似性质.
解答:解:(1)四面体任意三个面的面积之和大于第四个面的面积.
(2)四面体的中位面(过棱的中点的面)的面积等于第四个面的面积的四分之一.
(3)四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心.
(4)四面体的体积为V=
(S1+S2+S3+S4)r(r为四面体内切球的半径,S1,S2,S3,S4分别为四面体的四个面的面积).
(2)四面体的中位面(过棱的中点的面)的面积等于第四个面的面积的四分之一.
(3)四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心.
(4)四面体的体积为V=
| 1 |
| 3 |
点评:本题主要考查了类比推理,解题的关键是将平面的性质类比到空间,同时考查了分析问题和解决问题的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
映射f:X→Y是定义域到值域的函数,则下面四个结论中正确的是( )
| A、Y中的元素不一定有原象 | B、X中不同的元素在Y中有不同的象 | C、Y可以是空集 | D、以上结论都不对 |
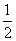 (a+b+c)r(r为三角形内切圆半径)。
(a+b+c)r(r为三角形内切圆半径)。 (a+b+c)r(r为三角形内切圆半径).
(a+b+c)r(r为三角形内切圆半径).