题目内容
在三角形中有下面的性质:(1)三角形的两边之和大于第三边;
(2)三角形的中位线等于第三边的一半,并且平行于第三边;
(3)三角形的三条内角平分线交于一点,且这个点是三角形的内心;
(4)三角形的面积为S=![]() (a+b+c)r(r为内切圆半径).
(a+b+c)r(r为内切圆半径).
请类比出四面体的有关性质.
思路点拨:利用三角形的有关性质,通过观察四面体的结构,比较二者的内在联系,从中类比出四面体的相似命题,提出猜想.
解:(1)四面体任意三个面的面积之和大于第四个面的面积.
(2)四面体的中位面的面积等于第四个面的面积的四分之一,且平行于第四个面.
(3)四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心.
(4)四面体的体积为V=![]() (S1+S2+S3+S4)r,r为内切球半径,S1、S2、S3、S4为四个面的面积.
(S1+S2+S3+S4)r,r为内切球半径,S1、S2、S3、S4为四个面的面积.
[一通百通]类比推理应从具体问题出发,通过观察、类比、归纳,提出猜想.通常情况下,平面图形中的面积与空间图形中的体积是类比的两类对象.可以类比的两类对象既有“共性”,又有“个性”.

练习册系列答案
相关题目
映射f:X→Y是定义域到值域的函数,则下面四个结论中正确的是( )
| A、Y中的元素不一定有原象 | B、X中不同的元素在Y中有不同的象 | C、Y可以是空集 | D、以上结论都不对 |
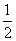 (a+b+c)r(r为三角形内切圆半径)。
(a+b+c)r(r为三角形内切圆半径)。 (a+b+c)r(r为三角形内切圆半径).
(a+b+c)r(r为三角形内切圆半径).