题目内容
过x轴上的动点A(a,0)的抛物线y=x2+1引两切线AP、AQ,P、Q为切点.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1k2为定值;
(2)求证:直线PQ过定点;
(3)若a≠0,试求S△APQ:|OA|的最小值.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1k2为定值;
(2)求证:直线PQ过定点;
(3)若a≠0,试求S△APQ:|OA|的最小值.
解:(1)设切点P(x1,y1),Q(x1,y1)
由题意可得,kAP= =
= ,由导数的几何意义可得,kAP=2x1,
,由导数的几何意义可得,kAP=2x1,
∴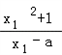 =2x1,整理可得
=2x1,整理可得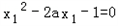 ,同理可得
,同理可得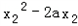 ﹣1=0,
﹣1=0,
从而可得x1,x2是方程x2﹣2ax﹣1=0的两根,
∴x=a±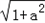 ,k1=
,k1= ,k2=
,k2=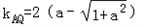 ,
,
∴k1k2=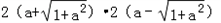 =﹣4,
=﹣4,
即k1k2为定值﹣4.
(2)设P(x1,y1),Q(x2,y2),
由于y'=2x,故切线AP的方程是:y﹣y1=2x1(x﹣x1),
则﹣y1=2x1(a﹣x1)=2x1a﹣2x12=2x1a﹣2(y1﹣1)
∴y1=2x1a+2,
同理y2=2x2a+2,
则直线PQ的方程是y=2ax+2,则直线PQ过定点(0,2).
(3) 即A(a,0)点到PQ的距离,
即A(a,0)点到PQ的距离,
要使 最小,就是使得A到直线PQ的距离最小,
最小,就是使得A到直线PQ的距离最小,
而A到直线PQ的距离d= =
=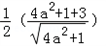 =
=
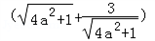 ≥
≥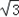 ,
,
当且仅当 ,即a2=
,即a2= 时取等号,
时取等号,
∴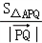 最小值为
最小值为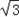 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
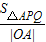 的最小值.
的最小值.