题目内容
过x轴上的动点A(a,0)引抛物线y=x2+1的两切线AP,AQ.P,Q为切点.(I)求切线AP,AQ的方程;
(Ⅱ)求证直线PQ过定点;
(III)若a≠0,试求
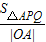 的最小值.
的最小值.
【答案】分析:(I)设切点P(x1,y1),Q(x2,y2),由题意可得,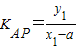 =
=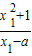 ,由导数的几何意义可得,KAP=2x1
,由导数的几何意义可得,KAP=2x1
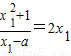 ,解方程可得切点,进而可求切线方程
,解方程可得切点,进而可求切线方程
(II)设P(x1,y1),Q(x2,y2),由题知y1=2x1a+2,y2=2x2a+2,可知直线PQ的方程是y=2ax+2,直线PQ过定点(0,2).
(Ⅲ)要使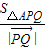 最小,就是使得A到直线PQ的距离最小,而A到直线PQ的距离
最小,就是使得A到直线PQ的距离最小,而A到直线PQ的距离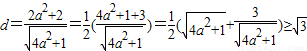 .由引入手能够推导出
.由引入手能够推导出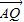 •
•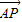 的最小值
的最小值
解答:解:(I)设切点P(x1,y1),Q(x2,y2)
由题意可得,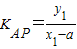 =
=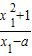 ,由导数的几何意义可得,KAP=2x1
,由导数的几何意义可得,KAP=2x1
∴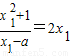
整理可得x12-2ax1-1=0,同理可得x22-2ax2-1=0
从而可得x1,x2是方程x2-2ax-1=0的两根
∴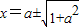 ,
,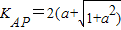 ,
,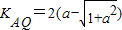
故可得切线AP方程为: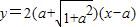 ,切线AQ的方程
,切线AQ的方程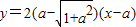
(II)设P(x1,y1),Q(x2,y2)
由于y'=2x,故切线AP的方程是:y-y1=2x1(x-x1)
则-y1=2x1(a-x1)=2x1a-2x12=2x1a-2(y1-1)
∴y1=2x1a+2,
同理y2=2x2a+2
则直线PQ的方程是y=2ax+2,则直线PQ过定点(0,2)
(Ⅲ)联立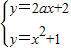 可得x2-2ax-1=0
可得x2-2ax-1=0
设P(x1,y1),Q(x2,y2)
,则x1+x2=2a,x1x2=-1
∴PQ=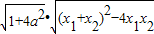 =
=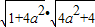
点A(a,0)到直线PQ的距离d=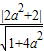
∴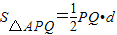 =
=
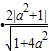 •
•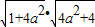 =
=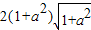
∴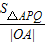 =
=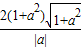
令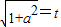 则t>1
则t>1
F(t)=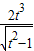 ,则令g(t)=F2(t)=
,则令g(t)=F2(t)=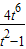 (t>1)
(t>1)
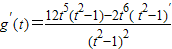 =
=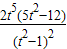 (t>1)
(t>1)
当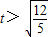 时,函数g(t)单调递增,即F(t)单调递增
时,函数g(t)单调递增,即F(t)单调递增
当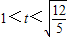 时,函数g(t)单调递减,即F(t)单调递减
时,函数g(t)单调递减,即F(t)单调递减
∴当t=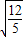 时,函数F(t)有最小值
时,函数F(t)有最小值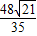 即
即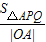 的最小值
的最小值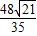
点评:本题主要考查直线与圆锥曲线的位置关系.解决这一类型题目的常用做法是把直线方程与圆锥曲线方程联立,再结合根于系数的关系求出交点坐标之间的关系.
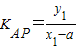 =
=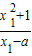 ,由导数的几何意义可得,KAP=2x1
,由导数的几何意义可得,KAP=2x1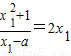 ,解方程可得切点,进而可求切线方程
,解方程可得切点,进而可求切线方程(II)设P(x1,y1),Q(x2,y2),由题知y1=2x1a+2,y2=2x2a+2,可知直线PQ的方程是y=2ax+2,直线PQ过定点(0,2).
(Ⅲ)要使
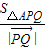 最小,就是使得A到直线PQ的距离最小,而A到直线PQ的距离
最小,就是使得A到直线PQ的距离最小,而A到直线PQ的距离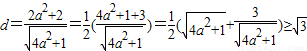 .由引入手能够推导出
.由引入手能够推导出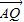 •
•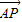 的最小值
的最小值解答:解:(I)设切点P(x1,y1),Q(x2,y2)
由题意可得,
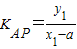 =
=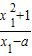 ,由导数的几何意义可得,KAP=2x1
,由导数的几何意义可得,KAP=2x1∴
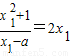
整理可得x12-2ax1-1=0,同理可得x22-2ax2-1=0
从而可得x1,x2是方程x2-2ax-1=0的两根
∴
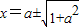 ,
,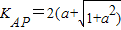 ,
,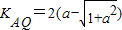
故可得切线AP方程为:
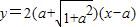 ,切线AQ的方程
,切线AQ的方程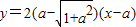
(II)设P(x1,y1),Q(x2,y2)
由于y'=2x,故切线AP的方程是:y-y1=2x1(x-x1)
则-y1=2x1(a-x1)=2x1a-2x12=2x1a-2(y1-1)
∴y1=2x1a+2,
同理y2=2x2a+2
则直线PQ的方程是y=2ax+2,则直线PQ过定点(0,2)
(Ⅲ)联立
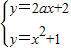 可得x2-2ax-1=0
可得x2-2ax-1=0设P(x1,y1),Q(x2,y2)
,则x1+x2=2a,x1x2=-1
∴PQ=
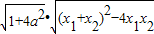 =
=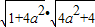
点A(a,0)到直线PQ的距离d=
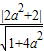
∴
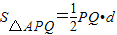 =
=
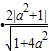 •
•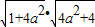 =
=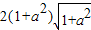
∴
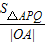 =
=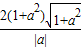
令
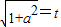 则t>1
则t>1F(t)=
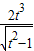 ,则令g(t)=F2(t)=
,则令g(t)=F2(t)=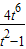 (t>1)
(t>1)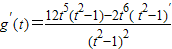 =
=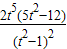 (t>1)
(t>1)当
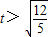 时,函数g(t)单调递增,即F(t)单调递增
时,函数g(t)单调递增,即F(t)单调递增当
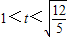 时,函数g(t)单调递减,即F(t)单调递减
时,函数g(t)单调递减,即F(t)单调递减∴当t=
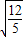 时,函数F(t)有最小值
时,函数F(t)有最小值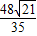 即
即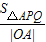 的最小值
的最小值
点评:本题主要考查直线与圆锥曲线的位置关系.解决这一类型题目的常用做法是把直线方程与圆锥曲线方程联立,再结合根于系数的关系求出交点坐标之间的关系.

练习册系列答案
相关题目