题目内容
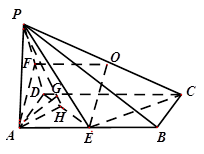
如图,已知在四棱锥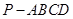 中,底面
中,底面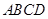 是矩形,
是矩形,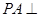 平面
平面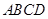 ,
,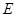 、
、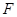 分别是
分别是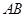 、
、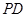 的中点.
的中点.
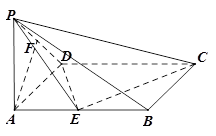
(Ⅰ)求证: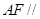 平面
平面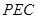 ;
;
(Ⅱ)若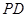 与平面
与平面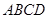 所成角为
所成角为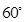 ,且
,且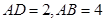 ,求点
,求点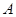 到平面
到平面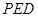 的距离.
的距离.
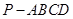 中,底面
中,底面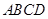 是矩形,
是矩形,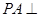 平面
平面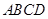 ,
,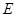 、
、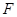 分别是
分别是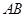 、
、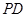 的中点.
的中点.
(Ⅰ)求证:
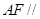 平面
平面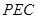 ;
;(Ⅱ)若
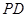 与平面
与平面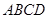 所成角为
所成角为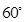 ,且
,且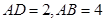 ,求点
,求点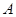 到平面
到平面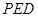 的距离.
的距离.(1)见试题解析;(2) .
.
 .
.试题分析:(I)要证明
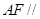 平面
平面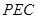 ,关键是在平面
,关键是在平面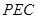 内找到一条与直线
内找到一条与直线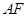 平行的直线,本题就想是否有一个过直线
平行的直线,本题就想是否有一个过直线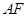 的平面与平面
的平面与平面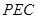 相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面
相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面 ,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取
,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取 中点
中点 ,然后连接
,然后连接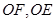 的方法);(2)由于
的方法);(2)由于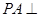 平面
平面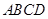 ,所以三棱锥
,所以三棱锥 的体积可以很快求出,从而本题可用体积法求点
的体积可以很快求出,从而本题可用体积法求点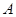 到平面
到平面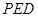 的距离,另外由于
的距离,另外由于 ,如果取
,如果取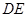 中点
中点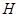 ,则有
,则有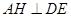 ,从而可得
,从而可得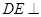 平面
平面 ,也即平面
,也即平面
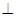 平面
平面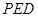 ,这时点
,这时点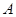 到平面
到平面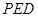 的垂线段可很快作出,从而迅速求出结论.
的垂线段可很快作出,从而迅速求出结论.试题解析:(I)证明:如图,取
 的中点
的中点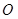 ,连接
,连接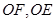 .
.
由已知得
 且
且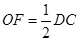 ,
,又
 是
是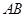 的中点,则
的中点,则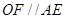 且
且 ,
,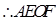 是平行四边形, ∴
是平行四边形, ∴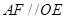
又
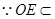 平面
平面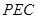 ,
,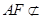 平面
平面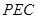
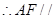 平面
平面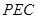
(II)设
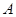 平面
平面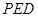 的距离为
的距离为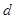 ,
,【法一】:因
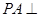 平面
平面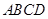 ,故
,故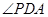 为
为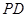 与平面
与平面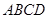 所成角,所以
所成角,所以 ,
,所以
 ,
,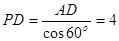 ,又因
,又因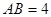 ,
,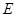 是
是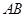 的中点所以
的中点所以 ,
, ,
, .
.作
 于
于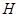 ,因
,因 ,则
,则 ,
,则
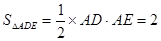 ,
,
因
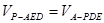 所以
所以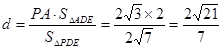
【法二】因
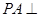 平面
平面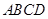 ,故
,故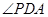 为
为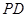 与平面
与平面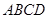 所成角,所以
所成角,所以 ,
,所以
 ,
,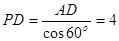 ,又因
,又因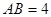 ,
,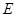 是
是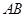 的中点所以
的中点所以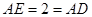 ,
, ,
, .
.作
 于
于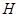 ,连结
,连结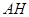 ,因
,因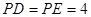 ,则
,则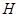 为
为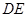 的中点,故
的中点,故
所以
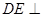 平面
平面 ,所以平面
,所以平面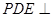 平面
平面 ,作
,作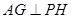 于
于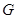 ,则
,则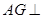 平面
平面 ,所以线段
,所以线段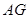 的长为
的长为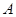 平面
平面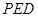 的距离.
的距离.又
 ,
,
所以
 .
.
练习册系列答案
相关题目
 中,
中,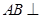 平面
平面 ,
,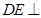 平面
平面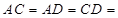
 ,
,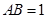 ,
,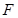 为
为 的中点.
的中点.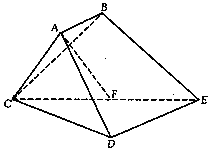
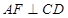 ;
;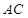 与平面
与平面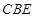 所成角的余弦值的大小.
所成角的余弦值的大小.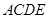 所在的平面垂直于平面
所在的平面垂直于平面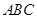 ,
,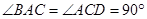 ,
,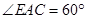 ,
,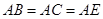 .
.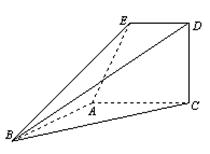
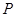 是直线
是直线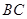 中点,证明
中点,证明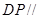 平面
平面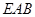 ;
;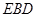 与平面
与平面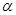 和
和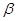 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: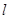 与
与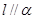 ;
;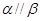 ;
;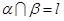 ,若
,若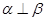 ;
;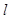 与平面
与平面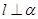 .
.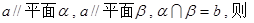
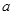 与
与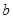 ( )
( )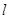 外两点作与直线
外两点作与直线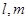 ,平面
,平面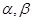 ,且
,且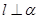 ,
,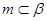 ,给出下列四个命题:
,给出下列四个命题: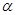 ∥
∥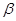 ,则
,则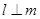 ;
;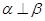 ,则
,则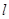 ∥
∥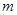 ;
; 是空间两条直线,
是空间两条直线,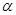 ,
,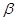 是空间两个平面,则下列选项中不正确的是( )
是空间两个平面,则下列选项中不正确的是( ) 时,“
时,“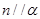 ”是“
”是“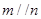 ”的必要不充分条件
”的必要不充分条件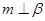 ”是“
”是“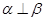 ”的充分不必要条件
”的充分不必要条件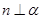 时, “
时, “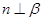 ”是“
”是“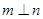 ”的充分不必要条件
”的充分不必要条件