题目内容
已知 .
.
(1)求 的极值,并证明:若
的极值,并证明:若 有
有 ;
;
(2)设 ,且
,且 ,
, ,证明:
,证明: ,
,
若 ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明);
(3)证明:若 ,则
,则 .
.
【答案】
(1)详见解析;(2) 详见解析;(3) 详见解析.
【解析】
试题分析:(1)利用求导探求函数的单调性,进而确定其极值;借助结论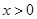 时
时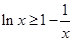 恒成立,证明
恒成立,证明 ;(2)借助第一问的结论,通过拼凑技巧进行构造要证明的不等式
;(2)借助第一问的结论,通过拼凑技巧进行构造要证明的不等式 ;(3)借助第二问的猜想结论,进行构造,利用对数运算进行化简整理即可得到证明的结论.
;(3)借助第二问的猜想结论,进行构造,利用对数运算进行化简整理即可得到证明的结论.
试题解析:(1) 则
则
当x∈(0,1)时 ,x∈(1,+∞)时
,x∈(1,+∞)时 ,
,
∴ 在(0,1)递增,在(1,+∞)递减,
在(0,1)递增,在(1,+∞)递减,
 2分
2分
∴当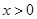 时
时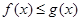 恒成立,即
恒成立,即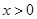 时
时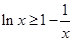 恒成立。
恒成立。
∴ 4分
4分
证明: ,
,
(2)证明:设 ,且
,且 ,令
,令 ,则
,则 ,且
,且
 ,
, ,
,
由(1)可知 ①
①
 ②
②
① +②
+② ,得
,得

∴ 8分
8分
猜想:若 ,且
,且 时有
时有
 9分
9分
(3)证明:令

由猜想结论得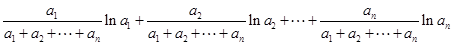

=
∴ ,
,
即有 。
14分
。
14分
考点:(1)函数的极值;(2)不等式的证明.

练习册系列答案
相关题目
 .
. 的极小值为1,求a的值.
的极小值为1,求a的值. ,都有
,都有 成立,求a的取值范围.
成立,求a的取值范围.
 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数 的根的个数问题:
的根的个数问题: 的取值范围
的取值范围
 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数 的根的个数问题:
的根的个数问题: 的取值范围
的取值范围
 的极大值和极小值,并画出函数
的极大值和极小值,并画出函数 的根的个数问题:
的根的个数问题: 的取值范围
的取值范围