题目内容
下列命题①若
 、
、 都是单位向量,则
都是单位向量,则 ;
;②终边在坐标轴上的角的集合是
 ;
;③若
 、
、 与
与 是三个非零向量,则
是三个非零向量,则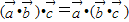 ;
;④正切函数在定义域上单调递增;
⑤向量
 与
与 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立.
成立.则错误的命题的序号是 .
【答案】分析:①利用单位向量的意义即可判断出;
②分别写出终边在x轴上的角的集合、终边在y轴上的角的集合,进而可得到终边在坐标轴上的角的集合;
③利用向量共线定理即可判断出;
④利用正切函数的单调性即可判断出;
⑤利用向量共线的充要条件即可判断出.
解答:解:①根据单位向量的定义可知: ,但是不一定有
,但是不一定有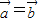 ,故不正确;
,故不正确;
②终边在x轴上的角的集合为{α|α=kπ,k∈Z},终边在y轴上的角的集合为{α|α=kπ ,k∈Z},故合在一起即为{α|
,k∈Z},故合在一起即为{α| ,n∈Z},故②正确;
,n∈Z},故②正确;
③∵ 、
、 与
与 是三个非零向量,∴
是三个非零向量,∴ 与
与 不一定共线,故
不一定共线,故 不一定成立,因此③不正确;
不一定成立,因此③不正确;
④正切函数y=tanx在每个区间 (k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确;
(k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确;
⑤向量 与
与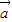 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立,而不是使得
成立,而不是使得 成立,故不正确.
成立,故不正确.
综上可知:①③④⑤都是错误的.
故答案为①③④⑤.
点评:熟练掌握单位向量的意义、终边在x轴上的角的集合及终边在y轴上的角的集合、向量共线的充要条件、正切函数的单调性是解题的关键.
②分别写出终边在x轴上的角的集合、终边在y轴上的角的集合,进而可得到终边在坐标轴上的角的集合;
③利用向量共线定理即可判断出;
④利用正切函数的单调性即可判断出;
⑤利用向量共线的充要条件即可判断出.
解答:解:①根据单位向量的定义可知:
 ,但是不一定有
,但是不一定有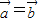 ,故不正确;
,故不正确;②终边在x轴上的角的集合为{α|α=kπ,k∈Z},终边在y轴上的角的集合为{α|α=kπ
 ,k∈Z},故合在一起即为{α|
,k∈Z},故合在一起即为{α| ,n∈Z},故②正确;
,n∈Z},故②正确;③∵
 、
、 与
与 是三个非零向量,∴
是三个非零向量,∴ 与
与 不一定共线,故
不一定共线,故 不一定成立,因此③不正确;
不一定成立,因此③不正确;④正切函数y=tanx在每个区间
 (k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确;
(k∈Z)上单调递增,但是在整个定义域上不单调,故④不正确;⑤向量
 与
与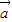 共线,当且仅当有唯一一个实数λ,使得
共线,当且仅当有唯一一个实数λ,使得 成立,而不是使得
成立,而不是使得 成立,故不正确.
成立,故不正确.综上可知:①③④⑤都是错误的.
故答案为①③④⑤.
点评:熟练掌握单位向量的意义、终边在x轴上的角的集合及终边在y轴上的角的集合、向量共线的充要条件、正切函数的单调性是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 ,则函数
,则函数 的图象不经过第三象限;
的图象不经过第三象限; 定义域是
定义域是 ,则
,则 的定义域是
的定义域是 ;
; 的单调减区间是
的单调减区间是
 ,那么
,那么 ;
; 是定义在
是定义在 上的不恒为
上的不恒为 的函数,且对于任意的
的函数,且对于任意的 ,都有
,都有 ,则函数
,则函数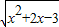 的单调减区间是(-∞,-1)
的单调减区间是(-∞,-1)