题目内容
下列命题正确的个数为①若0<a<1,则函数f(x)=loga(x+5)的图象不经过第三象限;
②已知函数y=f(x-1)定义域是[-2,3],则y=f(2x-1)的定义域是[-1,3];
③函数y=
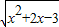 的单调减区间是(-∞,-1)
的单调减区间是(-∞,-1)④已知集合M={x|x+y=2},N={y|y=x2},那么M∩N=Φ;
⑤已知函数f(x)是定义在R上的不恒为0的函数,且对于任意的a,b∈R,都有f(ab)=af(b)+bf(a),则函数f(x)为奇函数.
【答案】分析:对于①,函数y=loga(x+5)的图象可看作是由函数y=logax的图象左移五个单位得到,结合函数y=logax的图象及平移规则,即可判断出图象不过的象限;对于②,求出函数y=f(2x-1)的定义域对比即可;对于③,定义域优先原则,对于④,分别求出集合M与N,再求交集可判定;对于⑤,先给a,b赋值,求得f(1)与f(-1),然后再利用条件探讨f(-x)与f(x)的关系,即可得到函数的奇偶性.
解答:解:对于①,函数y=loga(x+5)的图象可看作是由函数y=logax的图象左移五个单位得到,
由0<a<1,所以函数y=logax图象过一、四象限且递减,与横轴的交点过(1,0),
故函数y=loga(x+5)的图象也是递减的,且过(-4,0),
由此图象特征知,函数y=loga(x+5)的图象不经过第一象限,故①不正确
对于②,已知函数y=f(x-1)定义域是[-2,3],所以x-1∈[-3,2].
2x-1∈[-3,2],所以y=f(2x-1)的定义域是[-1, ],故②不正确.
],故②不正确.
对于③,函数y=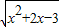 的定义域为(-∞,-3]∪[1,+∞),故减区间为(-∞,-3],故③不正确;
的定义域为(-∞,-3]∪[1,+∞),故减区间为(-∞,-3],故③不正确;
对于④,M={x|x+y=2}=R,N={y|y=x2}=[0,+∞),故M∩N≠Φ,故④不正确;
对于⑤,令a=b=1则f(1)=2f(1)则f(1)=0
令a=b=-1,则f(1)=-2f(-1)=0∴f(-1)=0
令a=x,b=-1,则f(-x)=-f(x)+xf(-1)=-f(x)
则f(x)为奇函数.故⑤正确
故正确有1个
故答案为:1
点评:本题主要考查了函数的定义域,单调性以及函数奇偶性的判断---定义法,在研究抽象函数的性质时注意赋值法的应用,同时考查了分析求解能力,属于基础题.
解答:解:对于①,函数y=loga(x+5)的图象可看作是由函数y=logax的图象左移五个单位得到,
由0<a<1,所以函数y=logax图象过一、四象限且递减,与横轴的交点过(1,0),
故函数y=loga(x+5)的图象也是递减的,且过(-4,0),
由此图象特征知,函数y=loga(x+5)的图象不经过第一象限,故①不正确
对于②,已知函数y=f(x-1)定义域是[-2,3],所以x-1∈[-3,2].
2x-1∈[-3,2],所以y=f(2x-1)的定义域是[-1,
 ],故②不正确.
],故②不正确.对于③,函数y=
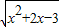 的定义域为(-∞,-3]∪[1,+∞),故减区间为(-∞,-3],故③不正确;
的定义域为(-∞,-3]∪[1,+∞),故减区间为(-∞,-3],故③不正确;对于④,M={x|x+y=2}=R,N={y|y=x2}=[0,+∞),故M∩N≠Φ,故④不正确;
对于⑤,令a=b=1则f(1)=2f(1)则f(1)=0
令a=b=-1,则f(1)=-2f(-1)=0∴f(-1)=0
令a=x,b=-1,则f(-x)=-f(x)+xf(-1)=-f(x)
则f(x)为奇函数.故⑤正确
故正确有1个
故答案为:1
点评:本题主要考查了函数的定义域,单调性以及函数奇偶性的判断---定义法,在研究抽象函数的性质时注意赋值法的应用,同时考查了分析求解能力,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
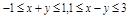 ,则
,则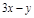 的范围是
的范围是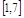 ;
;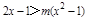 对满足
对满足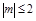 的所有m都成立,则x的范围是
的所有m都成立,则x的范围是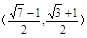 ;
;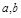 满足
满足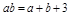 ,则
,则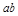 的取值范围是
的取值范围是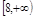
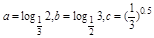 大小关系是
大小关系是