题目内容
已知F1、F2是双曲线
-y2=1的两个焦点，点M在双曲线上，若△F1MF2的面积为1，则
•
的值为（ ）
| x2 |
| 16 |
| MF1 |
| MF2 |
| A、1 | ||
| B、2 | ||
C、2
| ||
| D、0 |
分析：由△F1MF2的面积为1可以推导出点M到x轴的距离，从而得出M到原点的距离，可知点M在以F1F2为直径的圆上，得到
⊥
，最后得出
•
=0．
| MF1 |
| MF2 |
| MF1 |
| MF2 |
解答：解：∵双曲线
-y2=1，∴a=4，b=1，c=
．
设M（m，n）则△F1MF2的面积为1得：
×|n|×2c=1，∴|n|=
代入双曲线方程得：m2=
，
∴M到原点的距离
=
∴点M在以F1F2为直径的圆x2+y2=17上
故
⊥
则
•
的值为0．
故选D．
| x2 |
| 16 |
| 17 |
设M（m，n）则△F1MF2的面积为1得：
| 1 |
| 2 |
| 1 | ||
|
代入双曲线方程得：m2=
| 18×16 |
| 17 |
∴M到原点的距离
| m 2+n 2 |
| 17 |
∴点M在以F1F2为直径的圆x2+y2=17上
故
| MF1 |
| MF2 |
则
| MF1 |
| MF2 |
故选D．
点评：本题考查双曲线的性质及其应用，解题时要注意挖掘隐含条件，解答关键是利用两点间的距离公式得出点M在以F1F2为直径的圆上．
练习册系列答案
相关题目
已知F1，F2分别为双曲
-
=1(a＞0，b＞0)的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、（1，+∞） |
| B、（0，3] |
| C、（1，3] |
| D、（0，2] |
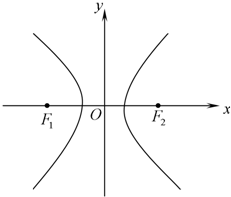
的左、右两个焦点，点P是双曲线上一点，且|PF1|．|PF2|=32，求∠F1PF2的大小．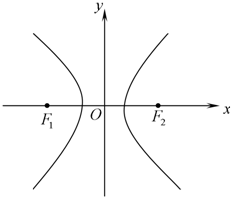
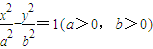的左、右焦点，P为双曲线左支上任一点，若
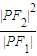的最小值为8a，则双曲线的离心率e的取值范围是（ ）
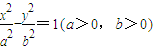的左、右焦点，P为双曲线左支上任一点，若
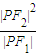的最小值为8a，则双曲线的离心率e的取值范围是（ ）