题目内容
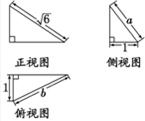 某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为( )
某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:三视图复原几何体是长方体的一个角,设出棱长,利用勾股定理,基本不等式,求出最大值.
解答:解:如图所示,可知AC=
,BD=1,BC=b,AB=a.
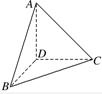
设CD=x,AD=y,
则x2+y2=6,x2+1=b2,y2+1=a2,
消去x2,y2得
.
a2+b2=8≥
,
所以(a+b)≤4,
当且仅当a=b=2时等号成立,此时x=
,y=
,
所以V=
×
×1×
×
=
.
故选D.
| 6 |

设CD=x,AD=y,
则x2+y2=6,x2+1=b2,y2+1=a2,
消去x2,y2得
| 3 |
| 8 |
a2+b2=8≥
| (a+b)2 |
| 2 |
所以(a+b)≤4,
当且仅当a=b=2时等号成立,此时x=
| 3 |
| 3 |
所以V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
故选D.
点评:本题考查三视图求体积,考查基本不等式求最值,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
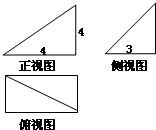
 某几何体的三视图如图,它的体积为( )
某几何体的三视图如图,它的体积为( ) (2012•大连二模)某几何体的三视图如图所示,根据图中尺寸(单位:m),可得该几何体的体积为
(2012•大连二模)某几何体的三视图如图所示,根据图中尺寸(单位:m),可得该几何体的体积为 (2012•烟台二模)已知某几何体的三视图如图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为
(2012•烟台二模)已知某几何体的三视图如图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为 已知某几何体的三视图如图所示,则几何体的体积为( )
已知某几何体的三视图如图所示,则几何体的体积为( )