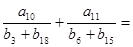题目内容
已知递增等差数列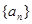 满足:
满足: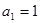 ,且
,且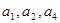 成等比数列.
成等比数列.
(1)求数列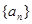 的通项公式
的通项公式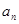 ;
;
(2)若不等式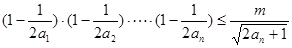 对任意
对任意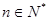 恒成立,试猜想出实数
恒成立,试猜想出实数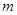 的最小值,并证明.
的最小值,并证明.
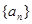 满足:
满足: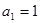 ,且
,且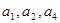 成等比数列.
成等比数列.(1)求数列
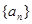 的通项公式
的通项公式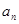 ;
;(2)若不等式
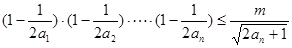 对任意
对任意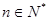 恒成立,试猜想出实数
恒成立,试猜想出实数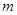 的最小值,并证明.
的最小值,并证明.(1)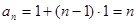 . (2)
. (2)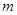 的最小值为
的最小值为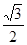 .
.
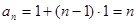 . (2)
. (2)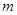 的最小值为
的最小值为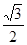 .
. 本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列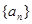 公差为
公差为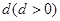 ,
,
由题意可知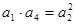 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于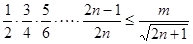 ,利用当
,利用当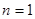 时,
时,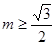 ;当
;当 时,
时,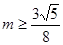 ;而
;而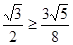 ,所以猜想,
,所以猜想,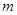 的最小值为
的最小值为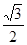 然后加以证明即可。
然后加以证明即可。
解:(1)设数列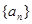 公差为
公差为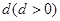 ,由题意可知
,由题意可知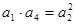 ,即
,即 ,
,
解得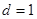 或
或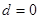 (舍去). …………3分
(舍去). …………3分
所以,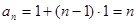 . …………6分
. …………6分
(2)不等式等价于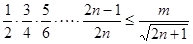 ,
,
当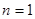 时,
时,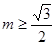 ;当
;当 时,
时,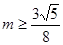 ;
;
而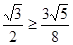 ,所以猜想,
,所以猜想,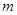 的最小值为
的最小值为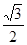 . …………8分
. …………8分
下证不等式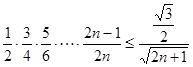 对任意
对任意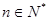 恒成立.
恒成立.
方法一:数学归纳法.
当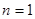 时,
时,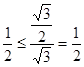 ,成立.
,成立.
假设当 时,不等式
时,不等式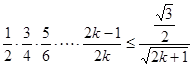 成立,
成立,
当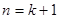 时,
时,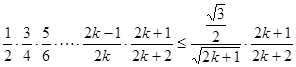 , …………10分
, …………10分
只要证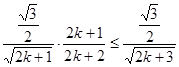 ,只要证
,只要证 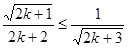 ,
,
只要证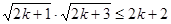 ,只要证
,只要证 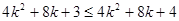 ,
,
只要证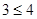 ,显然成立.所以,对任意
,显然成立.所以,对任意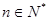 ,不等式
,不等式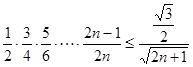 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证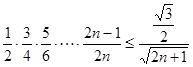
只要证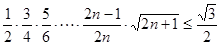 ,
,
设数列 的通项公式
的通项公式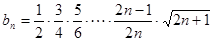 , …………10分
, …………10分
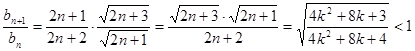 , …………12分
, …………12分
所以对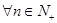 ,都有
,都有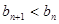 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而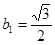 ,所以
,所以 恒成立,
恒成立,
故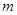 的最小值为
的最小值为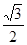 .
.
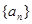 公差为
公差为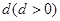 ,
,由题意可知
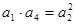 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于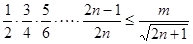 ,利用当
,利用当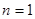 时,
时,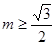 ;当
;当 时,
时,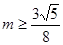 ;而
;而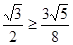 ,所以猜想,
,所以猜想,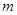 的最小值为
的最小值为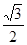 然后加以证明即可。
然后加以证明即可。解:(1)设数列
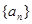 公差为
公差为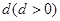 ,由题意可知
,由题意可知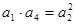 ,即
,即 ,
,解得
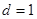 或
或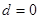 (舍去). …………3分
(舍去). …………3分所以,
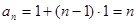 . …………6分
. …………6分(2)不等式等价于
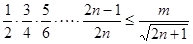 ,
,当
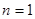 时,
时,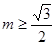 ;当
;当 时,
时,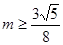 ;
;而
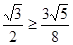 ,所以猜想,
,所以猜想,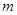 的最小值为
的最小值为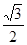 . …………8分
. …………8分下证不等式
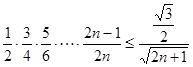 对任意
对任意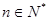 恒成立.
恒成立.方法一:数学归纳法.
当
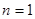 时,
时,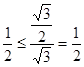 ,成立.
,成立.假设当
 时,不等式
时,不等式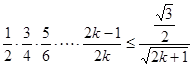 成立,
成立, 当
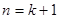 时,
时,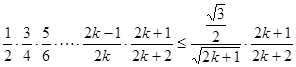 , …………10分
, …………10分只要证
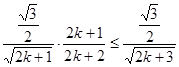 ,只要证
,只要证 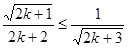 ,
,只要证
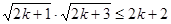 ,只要证
,只要证 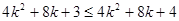 ,
,只要证
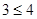 ,显然成立.所以,对任意
,显然成立.所以,对任意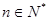 ,不等式
,不等式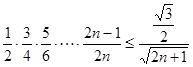 恒成立.…14分
恒成立.…14分方法二:单调性证明.
要证
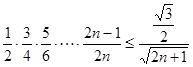
只要证
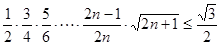 ,
, 设数列
 的通项公式
的通项公式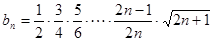 , …………10分
, …………10分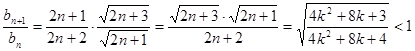 , …………12分
, …………12分所以对
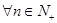 ,都有
,都有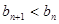 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.而
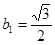 ,所以
,所以 恒成立,
恒成立,故
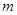 的最小值为
的最小值为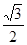 .
.
练习册系列答案
相关题目
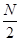 和后
和后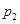 ;当2≤i≤n-2时,将Pi分成2i段,每段
;当2≤i≤n-2时,将Pi分成2i段,每段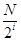 个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置.
个数,并对每段C变换,得到Pi+1,例如,当N=8时,P2=x1x5x3x7x2x6x4x8,此时x7位于P2中的第4个位置. 的通项公式
的通项公式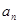 =( )
=( )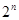
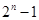
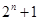

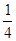
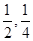
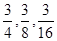
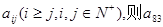 等于 .
等于 . 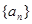 的前
的前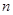 项和为
项和为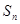 ,且
,且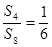 ,则
,则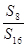 =( )
=( )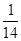
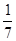
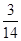
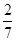
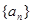 中,
中,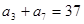 ,则
,则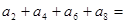 。
。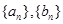 的前n项和分别为
的前n项和分别为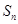 和
和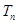 ,若
,若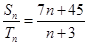 ,且
,且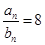 ,则n的值为__________.
,则n的值为__________.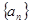 满足
满足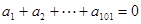 ,则 ( )
,则 ( )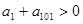
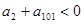
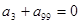
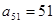
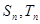 分别是等差数列
分别是等差数列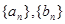 的前
的前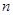 项和,且
项和,且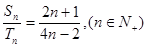 则
则