题目内容
已知函数f(x)=2sin(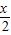 -
-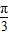 )
)(1)写出函数的振幅、周期、初相,并说明如何由正弦曲线得出它的图象;
(2)求函数y=f(x)的单调递减区间和对称轴的方程.
【答案】分析:(1)根据函数y=Asin(ωx+∅)中各个量的物理意义求得振幅、周期、初相.根据y=Asin(ωx+∅)的图象变换规律,可得如何由正弦曲线得出它的图象.
(2)令 2kπ+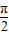 ≤
≤ x-
x-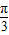 ≤2kπ+
≤2kπ+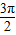 ,k∈z,求得x的范围,即可求得函数的减区间.令
,k∈z,求得x的范围,即可求得函数的减区间.令  x-
x-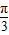 =kπ+
=kπ+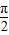 ,k∈z,求得x的值,即可求得函数的对称轴方程.
,k∈z,求得x的值,即可求得函数的对称轴方程.
解答:解:(1)由于函数f(x)=2sin(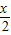 -
-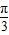 ),故函数的振幅为2,周期为T=
),故函数的振幅为2,周期为T=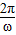 =
=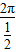 =4π,初相为-
=4π,初相为-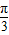 .
.
把正弦曲线y=sinx的图象上的各个点项右平移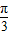 个单位,可得函数y=sin(x-
个单位,可得函数y=sin(x-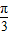 )的图象;
)的图象;
再把所得图象上各个点的横坐标变为原来的2倍,纵坐标不变,可得函数y=y=sin( x-
x-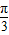 )的图象;
)的图象;
再把所得图象上各个点的纵坐标变为原来的2倍,横坐标不变,可得函数y=y=2sin( x-
x-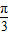 )的图象.
)的图象.
(2)令 2kπ+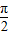 ≤
≤ x-
x-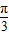 ≤2kπ+
≤2kπ+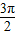 ,k∈z,求得 4kπ+
,k∈z,求得 4kπ+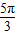 ≤x≤4kπ+
≤x≤4kπ+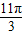 ,k∈z,
,k∈z,
故函数的减区间为[4kπ+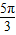 ,4kπ+
,4kπ+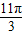 ],k∈z.
],k∈z.
令 x-
x- =kπ+
=kπ+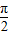 ,k∈z,求得x=2kπ+
,k∈z,求得x=2kπ+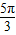 ,故函数的对称轴方程为x=2kπ+
,故函数的对称轴方程为x=2kπ+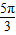 ,k∈z.
,k∈z.
点评:本题主要考查函数y=Asin(ωx+∅)中各个量的物理意义,y=Asin(ωx+∅)的图象变换规律,y=Asin(ωx+∅)的
对称性、单调性,属于中档题.
(2)令 2kπ+
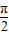 ≤
≤ x-
x-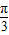 ≤2kπ+
≤2kπ+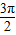 ,k∈z,求得x的范围,即可求得函数的减区间.令
,k∈z,求得x的范围,即可求得函数的减区间.令  x-
x-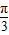 =kπ+
=kπ+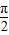 ,k∈z,求得x的值,即可求得函数的对称轴方程.
,k∈z,求得x的值,即可求得函数的对称轴方程.解答:解:(1)由于函数f(x)=2sin(
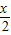 -
-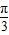 ),故函数的振幅为2,周期为T=
),故函数的振幅为2,周期为T=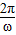 =
=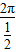 =4π,初相为-
=4π,初相为-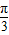 .
.把正弦曲线y=sinx的图象上的各个点项右平移
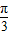 个单位,可得函数y=sin(x-
个单位,可得函数y=sin(x-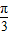 )的图象;
)的图象;再把所得图象上各个点的横坐标变为原来的2倍,纵坐标不变,可得函数y=y=sin(
 x-
x-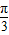 )的图象;
)的图象;再把所得图象上各个点的纵坐标变为原来的2倍,横坐标不变,可得函数y=y=2sin(
 x-
x-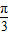 )的图象.
)的图象.(2)令 2kπ+
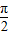 ≤
≤ x-
x-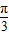 ≤2kπ+
≤2kπ+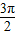 ,k∈z,求得 4kπ+
,k∈z,求得 4kπ+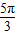 ≤x≤4kπ+
≤x≤4kπ+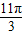 ,k∈z,
,k∈z,故函数的减区间为[4kπ+
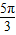 ,4kπ+
,4kπ+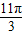 ],k∈z.
],k∈z.令
 x-
x- =kπ+
=kπ+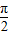 ,k∈z,求得x=2kπ+
,k∈z,求得x=2kπ+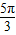 ,故函数的对称轴方程为x=2kπ+
,故函数的对称轴方程为x=2kπ+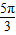 ,k∈z.
,k∈z.点评:本题主要考查函数y=Asin(ωx+∅)中各个量的物理意义,y=Asin(ωx+∅)的图象变换规律,y=Asin(ωx+∅)的
对称性、单调性,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目