题目内容

在数列{an}中，a1=-60，an+1=an+3，则|a1|+|a2|+…+|a30|=（　　）
分析：根据已知写出等差数列的通项公式，令an≥0，可得到n的范围，结合绝对值的几何意义及等差数列的求和公式即可求解
解答：解：{an}是等差数列，an=-60+3（n-1）=3n-63，
∴sn=
-60+3n-63
2
•n=
n(3n-123)
2

由an≥0，解得n≥21．
∴|a1|+|a2|+|a3|+…+|a30|
=-（a1+a2+…+a20）+（a21+…+a30）
=S30-2S20
=765
故选B
点评：此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值，本题的突破点是令通项公式大于等于0找出此数列从第22项开始变为正数．
练习册系列答案
相关题目
在数列{an}中，
a
 
1
=1，an=
1
2
an-1+1（n≥2），则数列{an}的通项公式为an=
2-21-n
2-21-n
．
在数列{an}中，a 1=
1
3
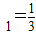，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
1
an
（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{
an
n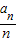
}的前n项和为Tn，证明：
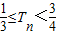1
3
≤Tn＜
3
4
．
在数列{an}中，a=
12
，前n项和Sn=n2an，求an+1．
在数列{an}中,a1=a,前n项和Sn构成公比为q的等比数列,________________.

(先在横线上填上一个结论,然后再解答)

在数列{an}中，a，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{}的前n项和为Tn，证明：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网