题目内容
设函数f(x)=xm+ax的导数f′(x)=2x+1,则数列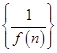 n∈(N*)的前n项和( )
n∈(N*)的前n项和( )
A.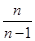 | B.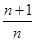 | C.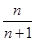 | D. |
C
解析试题分析:因为f'(x)=(xm+ax)′′=2x+1,∴m=2,a=1,∴f(x)=x2+x,所以数列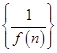 (n∈(N*)的前n项和为
(n∈(N*)的前n项和为
故可知结论为选C.
考点:本试题主要考查了导数的 运算以及裂项法求解数列的和的运用。
点评:若数列的通项公式为Cn=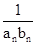 型时,可首先考虑裂项相消求和,这是一般的解题方法。
型时,可首先考虑裂项相消求和,这是一般的解题方法。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列 的通项公式
的通项公式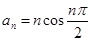 ,其前项和为
,其前项和为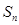 ,则
,则 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
已知数列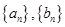 满足
满足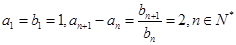 ,则数列
,则数列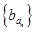 的前10项和为
的前10项和为
A.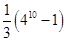 | B.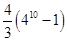 | C.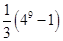 | D.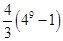 |
数列 的通项公式为
的通项公式为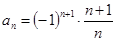 ,则
,则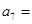 ( )
( )
| A.8 | B.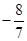 | C.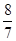 | D.7 |
若a、4、3a为等差数列的连续三项,则 的值为( )
的值为( )
| A.1025 | B.1023 | C.1062 | D.2047 |
 中,
中,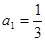 ,前
,前 项和
项和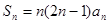 ,则数列
,则数列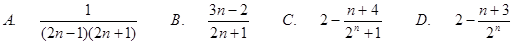
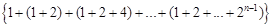 的前
的前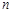 项和为_____________.
项和为_____________.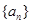 与
与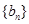 满足
满足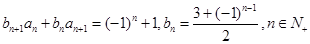 ,且
,且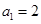 ,设数列
,设数列 项和为
项和为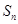 ,则
,则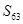 =.
=.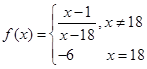 ,则
,则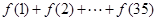 的值为 .
的值为 .