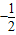题目内容
以抛物线x2=2y上点P(2,2)为切点的切线,与其准线交点的横坐标为( )
A.-
| B.-
| C.
| D.
|
由题意可得:抛物线方程为:y=
x2,
所以y′=x,
又因为切点为p(2,2),
所以切线的斜率为y′|x=2=2,
所以切线的方程为:2x-y-2=0.
因为抛物线的方程为:x2=2y,
所以抛物线的准线方程为:y=-
,
所以切线与其准线交点的横坐标为
.
故选C.
| 1 |
| 2 |
所以y′=x,
又因为切点为p(2,2),
所以切线的斜率为y′|x=2=2,
所以切线的方程为:2x-y-2=0.
因为抛物线的方程为:x2=2y,
所以抛物线的准线方程为:y=-
| 1 |
| 2 |
所以切线与其准线交点的横坐标为
| 3 |
| 4 |
故选C.

练习册系列答案
相关题目
以抛物线x2=2y上点P(2,2)为切点的切线,与其准线交点的横坐标为( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
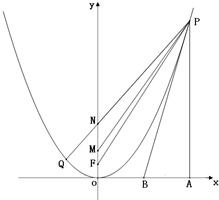 已知四点O(0,0),
已知四点O(0,0),