题目内容
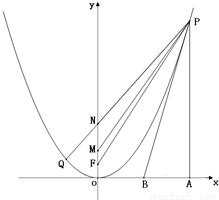
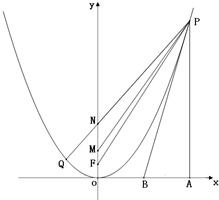 已知四点O(0,0),F(0,
已知四点O(0,0),F(0,| 1 |
| 2 |
(Ⅰ)当x0=3时,延长PN交抛物线于另一点Q,求∠POQ的大小;
(Ⅱ)当点P(x0,y0)(x0≠0)在抛物线x2=2y上运动时,
ⅰ)以MP为直径作圆,求该圆截直线y=
| 1 |
| 2 |
ⅱ)过点P作x轴的垂线交x轴于点A,过点P作该抛物线的切线l交x轴于点B.问:是否总有∠FPB=∠BPA?如果有,请给予证明;如果没有,请举出反例.
分析:(Ⅰ)当x0=3时,y0=
,P(3,
),kPN=
,把直线PN:y=
x+2代入x2=2y,得x2-
x-4=0,由此入手能求出∠POQ=90°.
(Ⅱ)ⅰ)以MP为直径的圆的圆心为(
,
y0+
),|MP|=
=
=
,
所以圆的半径r=
,圆心到直线y=
的距离d=|
y0+
-
|=|
y0|,由此能求出截得的弦长.
(Ⅱ)总有∠FPB=∠BPA.证明:y=
,y'=x,kl=y′|x=x0=x0,所以切线l的方程为y=x0x-
,令y=0,得x=
,所以点B的坐标为B(
,0),点B到直线PA的距离为d1=
,再求出直线PF的方程(x02-1)x-2x0y+x0=0,
所以点B到直线PF的距离为d2=
=
=
,由此知∠FPB=∠BPA.
| 9 |
| 2 |
| 9 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 3 |
(Ⅱ)ⅰ)以MP为直径的圆的圆心为(
| x0 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2y0+(y0-1)2 |
| y02+1 |
所以圆的半径r=
| 1 |
| 2 |
| y02+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)总有∠FPB=∠BPA.证明:y=
| x2 |
| 2 |
| ||
| 2 |
| x0 |
| 2 |
| x0 |
| 2 |
| |x0| |
| 2 |
所以点B到直线PF的距离为d2=
|(
| ||||
|
|(
| ||||
|
| |x0| |
| 2 |
解答:解:(Ⅰ)当x0=3时,y0=
,P(3,
),kPN=
直线PN:y=
x+2代入x2=2y,得x2-
x-4=0,x=-
,3,
所以Q(-
,
),
•
=3×(-
)+
×
=0,
所以∠POQ=90°(5分)
(Ⅱ)ⅰ)以MP为直径的圆的圆心为(
,
y0+
),|MP|=
=
=
,
所以圆的半径r=
,
圆心到直线y=
的距离d=|
y0+
-
|=|
y0|;
故截得的弦长l=2
=2
=1(10分)
(Ⅱ)总有∠FPB=∠BPA.(11分)
证明:y=
,y'=x,kl=y′|x=x0=x0,
所以切线l的方程为y-
=x0(x-x0),即y=x0x-
令y=0,得x=
,所以点B的坐标为B(
,0)(12分)
点B到直线PA的距离为d1=
,
下面求直线PF的方程
因为F(0,
),所以直线PF的方程为y-
=
(x-0),
整理得(x02-1)x-2x0y+x0=0
所以点B到直线PF的距离为d2=
=
=
,
所以d1=d2
所以∠FPB=∠BPA(15分)
| 9 |
| 2 |
| 9 |
| 2 |
| 5 |
| 6 |
直线PN:y=
| 5 |
| 6 |
| 5 |
| 3 |
| 4 |
| 3 |
所以Q(-
| 4 |
| 3 |
| 8 |
| 9 |
| OP |
| OQ |
| 4 |
| 3 |
| 9 |
| 2 |
| 8 |
| 9 |
所以∠POQ=90°(5分)
(Ⅱ)ⅰ)以MP为直径的圆的圆心为(
| x0 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2y0+(y0-1)2 |
| y02+1 |
所以圆的半径r=
| 1 |
| 2 |
| y02+1 |
圆心到直线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故截得的弦长l=2
| r2-d2 |
|
(Ⅱ)总有∠FPB=∠BPA.(11分)
证明:y=
| x2 |
| 2 |
所以切线l的方程为y-
| ||
| 2 |
| ||
| 2 |
令y=0,得x=
| x0 |
| 2 |
| x0 |
| 2 |
点B到直线PA的距离为d1=
| |x0| |
| 2 |
下面求直线PF的方程
因为F(0,
| 1 |
| 2 |
| 1 |
| 2 |
| ||||||
| x0 |
整理得(x02-1)x-2x0y+x0=0
所以点B到直线PF的距离为d2=
|(
| ||||
|
|(
| ||||
|
| |x0| |
| 2 |
所以d1=d2
所以∠FPB=∠BPA(15分)
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,注意公式的合理运用.

练习册系列答案
相关题目
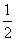 ),M(0,1),N(0,2),点P(x,y)在抛物线x2=2y上。
),M(0,1),N(0,2),点P(x,y)在抛物线x2=2y上。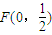 ,M(0,1),N(0,2).点P(x,y)在抛物线x2=2y上
,M(0,1),N(0,2).点P(x,y)在抛物线x2=2y上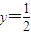 所得的弦长;
所得的弦长;