题目内容
已知命题p:“存在实数a,使直线x+ay-2=0与圆x2+y2=1有公共点”,命题q:“存在实数a,使点(a,1)在椭圆
+
=1内部”,若命题“p且?q”是真命题,求实数a的取值范围.
| x2 |
| 8 |
| y2 |
| 2 |
分析:先求命题p,q为真命题时a的范围,再根据复合命题真值表判断,若命题“p且?q”是真命题,则命题p,¬q都是真命题,即p真q假,从而求出a的范围.
真值表进行判断.
真值表进行判断.
解答:解:∵直线x+ay-2=0与圆x2+y2=1有公共点
∴
≤1⇒a2≥1,即a≥1或a≤-1,
命题p为真命题时,a≥1或a≤-1;
∵点(a,1)在椭圆
+
=1内部,
∴
+
<1 即a2<4,即-2<a<2,
命题q为真命题时,-2<a<2,
由复合命题真值表知:若命题“p且?q”是真命题,则命题p,¬q都是真命题
即p真q假,则
⇒a≥2或a≤-2.
故所求a的取值范围为(-∞,-2]∪[2,+∞).
∴
| 2 | ||
|
命题p为真命题时,a≥1或a≤-1;
∵点(a,1)在椭圆
| x2 |
| 8 |
| y2 |
| 2 |
∴
| a2 |
| 8 |
| 1 |
| 2 |
命题q为真命题时,-2<a<2,
由复合命题真值表知:若命题“p且?q”是真命题,则命题p,¬q都是真命题
即p真q假,则
|
故所求a的取值范围为(-∞,-2]∪[2,+∞).
点评:本题借助考查复合命题的真假判定,考查了直线与圆的位置关系,点与椭圆的位置关系,解决的关键是求简单命题为真时a的范围.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
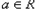 ,命题
,命题 实系数一元二次方程
实系数一元二次方程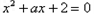 无实根;命题
无实根;命题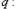 存在点
存在点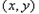 同时满足
同时满足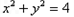 且
且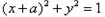 .试判断:命题p是命题q的什么条件(充分、必要、充分不必要、必要不充分、充要或既不充分也不必要条件)?请说明你的理由.
.试判断:命题p是命题q的什么条件(充分、必要、充分不必要、必要不充分、充要或既不充分也不必要条件)?请说明你的理由.