题目内容
16．已知线段AB=6，动点P，Q满足PA=1，QA=2QB，则PQ的取值范围是[0，10]．分析 以线段AB所在直线为x轴，AB的垂直平分线为y轴，建立坐标系，求出P，Q的轨迹方程，即可求出PQ的取值范围．
解答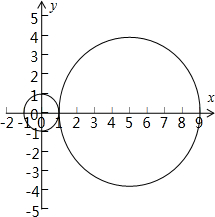 
解：以线段AB所在直线为x轴，AB的垂直平分线为y轴，建立如图所示的坐标系，则A（-3，0），B（3，0）
设Q（x，y），则
∴QA=2QB，
∴（x+3）2+y2=4（x-3）2+4y2，
即（x-5）2+y2=16，
又PA=1，P的方程为x2+y2=1，
∴两圆外切，
∴PQ的取值范围是[0，10]．
故答案为：[0，10]．
点评 本题考查轨迹方程，考查圆与圆的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知椭圆C的中心在原点，焦点在x轴上，离心率等于$\frac{{\sqrt{3}}}{2}$，它的一个顶点恰好在抛物线x2=8y的准线上．