题目内容
数列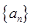 中,
中,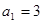 且
且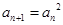 (
( 是正整数),则数列的通项公式
是正整数),则数列的通项公式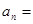 .
.

解析试题分析:根据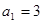 且
且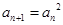 ,可知
,可知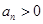 ,于是可得
,于是可得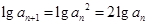 即
即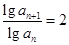 ,所以数列
,所以数列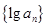 是以
是以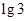 为首项,2为公比的等比数列,所以
为首项,2为公比的等比数列,所以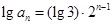 ,所以
,所以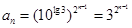 .
.
考点:1.数列的通项;2.等比数列的通项公式.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
题目内容
数列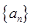 中,
中,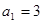 且
且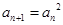 (
( 是正整数),则数列的通项公式
是正整数),则数列的通项公式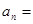 .
.

解析试题分析:根据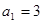 且
且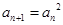 ,可知
,可知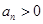 ,于是可得
,于是可得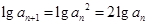 即
即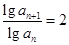 ,所以数列
,所以数列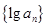 是以
是以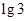 为首项,2为公比的等比数列,所以
为首项,2为公比的等比数列,所以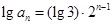 ,所以
,所以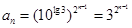 .
.
考点:1.数列的通项;2.等比数列的通项公式.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案