题目内容
(5分)(2011•广东)已知{an}是递增等比数列,a2=2,a4﹣a3=4,则此数列的公比q= .
2
解析试题分析:由已知{an}是递增等比数列,a2=2,我们可以判断此数列的公比q>1,又由a2=2,a4﹣a3=4,我们可以构造出一个关于公比q的方程,解方程即可求出公比q的值.
解:∵{an}是递增等比数列,
且a2=2,则公比q>1
又∵a4﹣a3=a2(q2﹣q)=2(q2﹣q)=4
即q2﹣q﹣2=0
解得q=2,或q=﹣1(舍去)
故此数列的公比q=2
故答案为:2
点评:本题考查的知识点是等比数列的通项公式,其中利用等比数列的通项公式及a2=2,a4﹣a3=4,构造出一个关于公比q的方程,是解答本题的关键.

练习册系列答案
相关题目
已知数列 的通项公式为
的通项公式为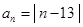 ,那么满足
,那么满足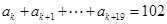 的整
的整 ( )
( )
| A.有3个 | B.有2个 | C.有1个 | D.不存在 |
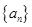 中,
中, 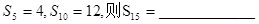
 的前n项和为
的前n项和为 ,那么该数列的通项公式为
,那么该数列的通项公式为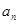 =_______.
=_______. 为数列
为数列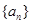 的前
的前 项和,
项和, ,
, ,其中
,其中 是常数.若对于任意的
是常数.若对于任意的 ,
,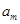 ,
,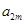 ,
, 成等比数列,则
成等比数列,则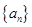 中,
中,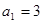 且
且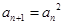 (
(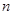 是正整数),则数列的通项公式
是正整数),则数列的通项公式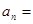 .
.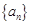 中,已知
中,已知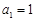 ,
, .设
.设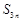 为该数列的前
为该数列的前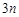 项和,
项和,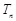 为数列
为数列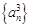 的前
的前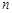 项和.若
项和.若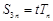 ,则实数
,则实数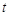 的值为 .
的值为 .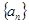 的前
的前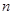 项积为
项积为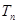 ,若
,若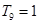 ,则
,则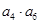 =__________.
=__________.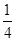 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.