题目内容
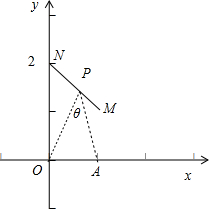
已知O(0,0),A(1,0),P为线段l:x+y=2,(0<x≤1)上的一动点.试求点P,使得P对O、A的视角∠APO最大.
分析:设∠APO=θ,则θ可看作PO到PA的角,由tanθ=
,化简变形为
,运用基本不等式求出它的最大值,即可得到θ的最大值以及此时点P的坐标.
| KPA- KPO |
| 1+KPA•KPO |
| 1 | ||
2(2-a)-3+
|
解答:解:设点P(a,2-a ),0<a≤1,设∠APO=θ,则θ可看作PO到PA的角.
由于PO的斜率为KPO=
,PA的斜率为 KPA=
,
由一条直线到另一条直线的夹角公式可得 tanθ=
=
=
=
=
=
≤
=1,当且仅当
=1时,即a=1时,等号成立.
故tanθ的 最大值为1,θ的最大值等于
.
故点P的坐标为( 1,1).
由于PO的斜率为KPO=
| 2-a |
| a |
| 2-a |
| a-1 |
由一条直线到另一条直线的夹角公式可得 tanθ=
| KPA- KPO |
| 1+KPA•KPO |
| ||||
1+
|
| a(2-a)-(a-1)(2-a) |
| a(a-1)+(2-a)2 |
=
| 2-a |
| 2a2-5a+4 |
| 2-a |
| 2(2-a)2-3(2-a)+2 |
| 1 | ||
2(2-a)-3+
|
| 1 |
| 4-3 |
| 2 |
| 2-a |
故tanθ的 最大值为1,θ的最大值等于
| π |
| 4 |
故点P的坐标为( 1,1).

点评:本题主要考查一条直线到另一条直线的夹角公式的应用,以及基本不等式的应用,式子的变形是解题的难点,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目