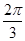题目内容
双曲线 的右焦点为F,右顶点为P,点B(0,b),离心率
的右焦点为F,右顶点为P,点B(0,b),离心率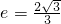 ,则双曲线C是下图中
,则双曲线C是下图中
- A.
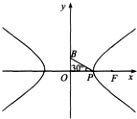
- B.
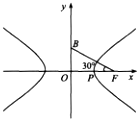
- C.
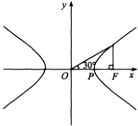
- D.
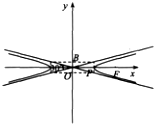
A
分析:根据双曲线的离心率,可求得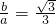 ,再一一验证,即可得到结论.
,再一一验证,即可得到结论.
解答:∵离心率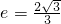 ,
,
∴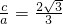
∴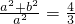
∴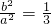
∴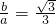
图A中,右顶点为P,点B(0,b),∴∠BPO=30°,故A成立;
图B中,右焦点为F,点B(0,b),故B不成立;
图C中,过F垂直于x轴的直线交椭圆于点B,则B(c, ),tan∠BOF=
),tan∠BOF=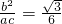 ,故C不成立;
,故C不成立;
图D,∵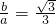 ,∴D不成立
,∴D不成立
故选A.
点评:本题考查的重点是双曲线的离心率,解题的关键是根据离心率得到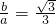 ,属于基础题.
,属于基础题.
分析:根据双曲线的离心率,可求得
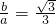 ,再一一验证,即可得到结论.
,再一一验证,即可得到结论.解答:∵离心率
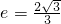 ,
,∴
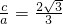
∴
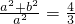
∴
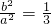
∴
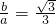
图A中,右顶点为P,点B(0,b),∴∠BPO=30°,故A成立;
图B中,右焦点为F,点B(0,b),故B不成立;
图C中,过F垂直于x轴的直线交椭圆于点B,则B(c,
 ),tan∠BOF=
),tan∠BOF=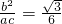 ,故C不成立;
,故C不成立;图D,∵
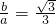 ,∴D不成立
,∴D不成立故选A.
点评:本题考查的重点是双曲线的离心率,解题的关键是根据离心率得到
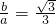 ,属于基础题.
,属于基础题. 
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
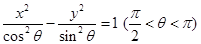 的右焦点为F,P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于
的右焦点为F,P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于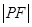 ,则
,则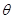 的值为( )
的值为( )
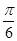 B.
B.
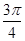 C.
C.
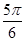 D.
D.