Question

已知函数f（x）=

x

1+x

，
（1）画出f（x）的草图；
（2）由图象指出f（x）的单调区间；
（3）设a＞0，b＞0，c＞0，a+b＞c，证明：f（a）+f（b）＞f（c）．

Answer 1

分析：（1）化函数为f(x)=1-

1

x+1

，可知它是由反比例函数y=

-1

x

平移而得，作出反比例函数y=

-1

x

的草图，再作相应的平移可得f（x）的草图；
（2）根据（1）中图象的特征，可得出函数的两个单调增区间；
（3）根据函数f（x）的单调性，结合不等式的放缩，可以得出欲证的结论．

解答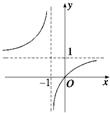：解：（1）由f（x）=

x

1+x

得f（x）=1-

1

x+1

．
∴f（x）的图象可由y=-

1

x

的图象向左平移1个
单位，再向上平移1个单位得到如图．

（2）解由图象知（-∞，-1），（-1，+∞）均为f（x）的单调增区间．

（3）证明∵f（x）在（-1，+∞）为增函数，
∵

a

1+a

＞

a

1+a+b

＞0 ，

b

1+b

＞

b

1+a+b

＞0，a+b＞c＞0，
∴f（a）+f（b）=

a

1+a

+

b

1+b

＞

a+b

1+a+b

＞

c

1+c

，
而f（c）=

c

1+c

，
∴f（a）+f（b）＞f（c）．

点评：本题考查了函数的图象与单调性的理解，同时还考查了用放缩法证明不等式，属于中档题．