题目内容
设函数 f(x)=x2-bx+| c2 | 4 |
（1）若b和c分别是先后抛掷一枚骰子得到的点数，求对任意x∈R，f（x）＞0恒成立的概率．
（2）若b是从区间[0，8]（3）任取得一个数，c是从[0，6]（4）任取的一个数，求函数f（x）的图象与x轴有交点的概率．
分析：（1）本题是一个等可能事件的概率，试验发生包含的事件数是6×6=36种结果，f（x）＞0要满足判别式小于0，列举出结果．
（2）利用几何概型的计算概率的方法解决本题，关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积，通过相除的方法完成本题的解答．
（2）利用几何概型的计算概率的方法解决本题，关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积，通过相除的方法完成本题的解答．
解答：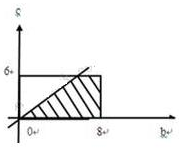
解：（1）由点（b，c）组成的点共36tkh，
设A={任意x∈R，f（x）＞0恒成立}即△=b2-c2＜0，
∴b＜c，A中包含基本事件15个，
∴P（A）=
=
；
（2）（b，c）所在的区域Ω={（b，c）|0≤b≤8，0≤c≤6}
若使函数f（x）的图象与x轴有交点，
则b≥c≥0．
∴事件B={（b，c）|b＞c，0≤b≤8，0≤c≤6}如图，
∴P（B）=
=
．
解：（1）由点（b，c）组成的点共36tkh，设A={任意x∈R，f（x）＞0恒成立}即△=b2-c2＜0，
∴b＜c，A中包含基本事件15个，
∴P（A）=
| 15 |
| 36 |
| 5 |
| 12 |
（2）（b，c）所在的区域Ω={（b，c）|0≤b≤8，0≤c≤6}
若使函数f（x）的图象与x轴有交点，
则b≥c≥0．
∴事件B={（b，c）|b＞c，0≤b≤8，0≤c≤6}如图，
∴P（B）=
48-
| ||
| 48 |
| 5 |
| 8 |
点评：本题考查等可能事件的概率，在解题过程中主要通过比例的方法计算概率的问题，考查学生分析问题解决问题的能力，考查学生几何图形面积的计算方法，属于基本题型．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目