题目内容
设函数f(x)=p(x-| 1 |
| x |
| 2e |
| x |
(1)若f(x)在其定义域内为单调函数,求p的取值范围;
(2)若直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象相切于点(1,0),求p的值;
(3)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.
分析:(1)求导f’(x)=
,要使“f(x)为单调增函数”,转化为“f’(x)≥0恒成立”,再转化为“p≥
=
恒成立”,由最值法求解.同理,要使“f(x)为单调减函数”,转化为“f’(x)≤0恒成立”,再转化为“p≤
=
恒成立”,由最值法求解,最后两个结果取并集.
(2)由“函数f(x)的图象相切于点(1,0”求得切线l的方程,再由“l与g(x)图象相切”得到(p-1)x2-(p-1)x-e=0
由判别式求解即可.
(3)因为“在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立”,要转化为“f(x)max>g(x)min”解决,易知g(x)=
在[1,e]上为减函数,所以g(x)∈[2,2e],①当p≤0时,f(x)在[1,e]上递减;②当p≥1时,f(x)在[1,e]上递增;③当0<p<1时,两者作差比较.
| px2-2x+p |
| x2 |
| 2x |
| x2+1 |
| 2 | ||
x+
|
| 2x |
| x2+1 |
| 2 | ||
x+
|
(2)由“函数f(x)的图象相切于点(1,0”求得切线l的方程,再由“l与g(x)图象相切”得到(p-1)x2-(p-1)x-e=0
由判别式求解即可.
(3)因为“在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立”,要转化为“f(x)max>g(x)min”解决,易知g(x)=
| 2e |
| x |
解答:解:(1)∵f’(x)=
,要使f(x)为单调增函数,须f’(x)≥0恒成立,
即px2-2x+p≥0恒成立,即p≥
=
恒成立,又
≤1,
所以当p≥1时,f(x)在(0,+∞)为单调增函数.
要使f(x)为单调减函数,须f’(x)≤0恒成立,
即px2-2x+0≤0恒成立,即p≤
=
恒成立,又
>0,
所以当p≤0时,f(x)在(0,+∞)为单调减函数.
综上所述,f(x)在(0,+∞)为单调函数,p的取值范围为p≥1或p≤0(4分)
(2)∵f’(x)=p+
-
,∴f’(1)=2(p-1),设直线l:y=2(p-1)(x-1),
∵l与g(x)图象相切,
∴y=2(p-1)(x-1)
得(p-1)(x-1)=
,即(p-1)x2-(p-1)x-e=0
y=
当p=1时,方程无解;当p≠1时由△=(p-1)2-4(p-1)(-e)=0,
得p=1-4e,综上,p=1-4e(4分)
(3)因g(x)=
在[1,e]上为减函数,所以g(x)∈[2,2e]
①当p≤0时,由(1)知f(x)在[1,e]上递减?f(x)max=f(1)=0<2,不合题意
②当p≥1时,由(1)知f(x)在[1,e]上递增,f(1)<2,又g(x)在[1,e]上为减函数,
故只需f(x)max>g(x)min,x∈[1,e],
即:f(e)=p(e-
)-2lne>2?p>
.
③当0<p<1时,因x-
≥0,x∈[1,e]
所以f(x)=p(x-
)-2lnx≤(x-
)-2lnx≤e-
-2lne<2不合题意
综上,p的取值范围为(
,+∞)(5分)
| px2-2x+p |
| x2 |
即px2-2x+p≥0恒成立,即p≥
| 2x |
| x2+1 |
| 2 | ||
x+
|
| 2 | ||
x+
|
所以当p≥1时,f(x)在(0,+∞)为单调增函数.
要使f(x)为单调减函数,须f’(x)≤0恒成立,
即px2-2x+0≤0恒成立,即p≤
| 2x |
| x2+1 |
| 2 | ||
x+
|
| 2 | ||
x+
|
所以当p≤0时,f(x)在(0,+∞)为单调减函数.
综上所述,f(x)在(0,+∞)为单调函数,p的取值范围为p≥1或p≤0(4分)
(2)∵f’(x)=p+
| p |
| x2 |
| 2 |
| x |
∵l与g(x)图象相切,
∴y=2(p-1)(x-1)
得(p-1)(x-1)=
| e |
| x |
y=
| 2e |
| x |
当p=1时,方程无解;当p≠1时由△=(p-1)2-4(p-1)(-e)=0,
得p=1-4e,综上,p=1-4e(4分)
(3)因g(x)=
| 2e |
| x |
①当p≤0时,由(1)知f(x)在[1,e]上递减?f(x)max=f(1)=0<2,不合题意
②当p≥1时,由(1)知f(x)在[1,e]上递增,f(1)<2,又g(x)在[1,e]上为减函数,
故只需f(x)max>g(x)min,x∈[1,e],
即:f(e)=p(e-
| 1 |
| e |
| 4e |
| e2-1 |
③当0<p<1时,因x-
| 1 |
| x |
所以f(x)=p(x-
| 1 |
| x |
| 1 |
| x |
| 1 |
| e |
综上,p的取值范围为(
| 4e |
| e2-1 |
点评:本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.

练习册系列答案
相关题目
 )-2lnx,g(x)=
)-2lnx,g(x)=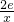 (p是实数,e为自然对数的底数)
(p是实数,e为自然对数的底数)