题目内容
20.已知函数f(x)=$\frac{{e}^{x}+a}{{e}^{x}+b}$是定义在上R的奇函数,则b的值为1.分析 由奇函数可得f(-x)+f(x)=0,代入整理由多项式系数相等可得ab的方程组,解方程组可得.
解答 解:∵函数f(x)=$\frac{{e}^{x}+a}{{e}^{x}+b}$是定义在上R的奇函数,
∴f(-x)+f(x)=0,即$\frac{{e}^{-x}+a}{{e}^{-x}+b}$+$\frac{{e}^{x}+a}{{e}^{x}+b}$=0,
∴$\frac{1+a{e}^{x}}{1+b{e}^{x}}$+$\frac{{e}^{x}+a}{{e}^{x}+b}$=0,即(1+aex)(ex+b)+(1+bex)(ex+a)=0,
整理可得(a+b)(ex)2+2(ab+1)ex+a+b=0
∴a+b=0且ab+1=0,解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$,
当$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$时,函数的解析式为f(x)=$\frac{{e}^{x}+1}{{e}^{x}-1}$,定义域为{x|x≠0},不合题意.
故答案为:1.
点评 本题考查函数的奇偶性,涉及方程组的解法,属基础题.

练习册系列答案
相关题目
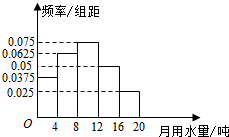 为提倡市民节约用水,中国水利部确定每年的3月22日至28日为“中国水周”,某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.
为提倡市民节约用水,中国水利部确定每年的3月22日至28日为“中国水周”,某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.