题目内容

设[x]表示不超过x的最大整数，如[2]=2，[
5
4
]=1，对于给定的n∈N*，定义Cnx=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则C
3
28
=
 
；当x∈[2，3）时，函数Cx8的值域是
 
．
分析：对于题目中新定义的：“Cnx=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
”理解是解决此题的问题，如求
C
3
2
8
，它是由一个分式的分子和分母两部分构成，分子是8，分母是
3
2
的分数．按此理解将函数Cx8的值域问题转化成一个函数的值域求解．
解答：解：当x=
3
2
时，[
3
2
]=1，
C
3
2
8
=
8
3
2
=
16
3
；
当x∈[2，3）时，[x]=2，Cxn=
n(n-1)
x(x-1)
，
Cx8=
8×7
x(x-1)
=
56
x(x-1)
．
又∵当x∈[2，3）时，f（x）=x（x-1）∈[2，6），
∴
56
x(x-1)
∈（
28
3
，28），∴Cx8∈（
28
3
，28]．
故答案为：
16
3
，（
28
3
，28]．
点评：本题是一道创新题，新的高考，每年均会出现一定新颖的题目，我们只要认真审题，细心研究，活用基础知识，把握数学思想、数学方法，构建知识结构和认知结构，实现知识到能力的转化．
练习册系列答案
相关题目
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
C
x
n
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数
C
x
8
的值域是（　　）
A、[
16
3
，28]
B、[
16
3
，56)
C、(4，
28
3
)∪[28，56）
D、(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数（如：[1]=1，[
5
2
]=2），则定义在[2，4）的函数f（x）=x[x]-ax（其中a为常数，且a≤4）的值域为（　　）
A、[4-2a，64-4a）
B、[4-2a，9-3a）∪[27-3a，64-4a）
C、[9-3a，64-4a）
D、[4-2a，9-3a]∪（27-3a，64-4a]
（2010•台州二模）设[x]表示不超过x的最大整数（如[2]=2，[1.3]=1），已知函数f(x)=
[x+
1
2
]
[x]+
1
2
（x≥0），当f（x）＜1时，实数x的取值范围是
{x|k≤x＜k+
1
2
，k∈N}
{x|k≤x＜k+
1
2
，k∈N}
．
设[x]表示不超过x的最大整数（如[2]=2，[
5
4
]=1），对于给定的n∈N*，定义
Cxn
=
n(n-1)…(n-[x]+1)
x(x-1)…(x-[x]+1)
，x∈[1，+∞），则当x∈[
3
2
，3)时，函数C8x的值域是（　　）
A．[
16
3
，28]		B．[
16
3
，56)
C．(4，
28
3
)∪[28，56）		D．(4，
16
3
]∪(
28
3
，28]
设[x]表示不超过x的最大整数，（如[2]=2，=1），对于给定的n∈N+，定义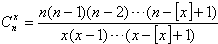，x∈[1，+∞），则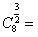（    ），当x∈[2，3）时，函数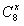的值域是（    ）。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网