题目内容
已知平面内点M(﹣3,2),N(5,﹣4),l是经过点A(﹣1,﹣2)且与MN垂直的直线,动点P(x,y)满足![]() .
.
(1)求直线l的方程与动点P的轨迹Σ的方程;
(2)在轨迹Σ上任取一点P,求P在直线l右下方的概率.
解答:
解:(1)由题意![]() ,
,![]() …(2分),
…(2分),
所以直线l的方程为![]() ,即4x﹣3y﹣2=0…(3分),
,即4x﹣3y﹣2=0…(3分),
又![]() ,
,![]() …(4分),
…(4分),
由![]() 得(﹣3﹣x)(5﹣x)+(2﹣y)(﹣4﹣y)=﹣21…(5分),
得(﹣3﹣x)(5﹣x)+(2﹣y)(﹣4﹣y)=﹣21…(5分),
整理得,轨迹方程为(x﹣1)2+(y+1)2=4…(6分)
(2)轨迹Σ是圆心为C(1,﹣1)、半径r=2的圆…(7分),
C到直线l的距离![]() …(8分),
…(8分),
所以d=1<r,直线l与圆Σ相交…(9分),
设交点为E、F,则![]() …(10分),所以
…(10分),所以![]() …(11分),
…(11分),
所以圆C的优弧EF的长为![]() …(12分),
…(12分),
因为P在直线l右下方,所以P在优弧EF上,所求概率为P=![]() =
=![]() …(14分)
…(14分)

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
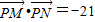 .
.