题目内容

设x≥1，求函数y=
(x+2)(x+3)x+1
的最小值．
分析：将函数进行整理，利用基本不等式进行求解即可．
解答：解：∵y=
(x+2)(x+3)
x+1
，
∴设t=x+1，
∵x≥1，
∴t≥2，
则函数等价为y=
(t+1)(t+2)
t
=
t2+3t+2
t
=t+
2
t
+3，
∵函数y=t+
2
t
+3在[
2
，+∞）上单调递增，
∴函数y=t+
2
t
+3在[2，+∞）上单调递增，
∵t≥2，
∴f（t）≥f（2）=2+
2
2
+3=6，
故答案为：6
点评：本题主要考查函数最值的计算，利用分式函数的特点转化为基本不等式性质是解决本题的关键，当基本不等式不成立是，要注意使用函数y=x+
a
x
，a＞0型的单调性的性质来解决．
练习册系列答案
相关题目
设函数f(x)=x2ex-1-
1
3
x3-x2(x∈R)．
（1）求函数y=f（x）的单调区间；
（2）求y=f（x）在[-1，2]上的最小值；
（3）当x∈（1，+∞）时，用数学归纳法证明：?n∈N*，ex-1＞
xn
n!
．
设x＞-1，求函数y=
(x+5)(x+2)x+1
的最小值．
（2012•浦东新区一模）设函数T(x)=
2x，  0≤x＜
1
2
2(1-x)，  
1
2
≤x≤1

（1）求函数y=T（sin（
π
2
x））和y=sin（
π
2
T（x））的解析式；
（2）是否存在非负实数a，使得aT（x）=T（ax）恒成立，若存在，求出a的值；若不存在，请说明理由；
（3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
①当x∈[0，
1
2n
]时，求y=Tn（x）的解析式；
已知下面正确的命题：当x∈[
i-1
2n
，
i+1
2n
]（i∈N*，1≤i≤2n-1）时，都有Tn（x）=Tn（
i
2n-1
-x）恒成立．
②对于给定的正整数m，若方程Tm（x）=kx恰有2m个不同的实数根，确定k的取值范围；若将这些根从小到大排列组成数列{xn}（1≤n≤2m），求数列{xn}所有2m项的和．

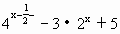设0≤x≤1，求函数y＝的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网