题目内容
12．已知f（x）在R上为奇函数，且f（x+4）=f（x），当x∈（0，2）时，f（x）=2x，则f（7）=（ ）| A． | -2 | B． | 2 | C． | 98 | D． | -98 |
分析 通过函数的周期以及函数的奇偶性，化简f（7），结合已知x∈（0，2）时，f （x）=2x，代入即可求解
解答 解：∵f（x+4）=f（x）函数的周期为4，
又∵函数f（x）为奇函数，
∴f（7）=f（-1+8）=f（-1）=-f（1），
∵x∈（0，2）时，f （x）=2x，
∴f（1）=2，
∴f（7）=-f（1）=-2．
故选：A
点评 本题主要考查了函数的奇偶性及函数的周期性在函数的函数值的求解中的综合应用．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
2．函数y=3+loga（2x+3）的图象必经过定点P的坐标为（ ）
| A． | （-1，3） | B． | （-1，4） | C． | （0，1） | D． | （2，2） |
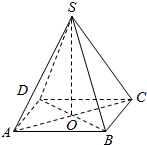如图，四棱锥S-ABCD的侧倰均相等，底面ABCD为平行四边形，其对角线交点为O．