题目内容
(本小题满分12分)已知函数 。
。
 如果
如果 ,函数在区间
,函数在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
 当
当 时,不等式
时,不等式 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
【答案】
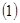
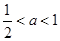 ;
;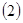
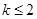 。
。
【解析】
试题分析:(1)因为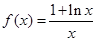 , x >0,则
, x >0,则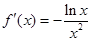 , (1分)
, (1分)
当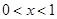 时,
时,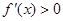 ;当
;当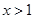 时,
时,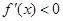 .
.
所以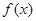 在(0,1)上单调递增;在
在(0,1)上单调递增;在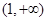 上单调递减,
上单调递减,
所以函数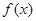 在
在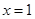 处取得极大值.
处取得极大值.
因为函数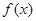 在区间
在区间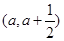 (其中
(其中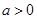 )上存在极值,
)上存在极值,
所以 解得
解得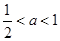 .
.
(2)不等式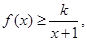 即为
即为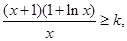 记
记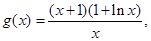
所以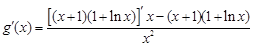
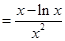
令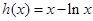 ,则
,则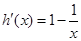 ,
, 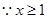 ,
,
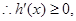
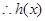 在
在 上单调递增,
上单调递增, 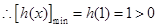 ,
,
从而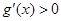 ,故
,故 在
在 上也单调递增,所以
上也单调递增,所以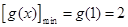 ,
,
所以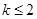 .
.
考点:利用导数来研究函数的单调性和极值。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: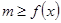 在
在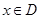 上恒成立
上恒成立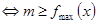 ;思路2:
;思路2: 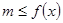 在
在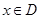 上恒成立
上恒成立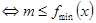 。
。

练习册系列答案
相关题目