题目内容
已知α,β为三角形内角,则“α>β”是“sinα>sinβ”的( )A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:由正弦定理知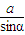 =
=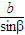 =2R,故sinA>sinB?a>b?A>B,故可得结论.
=2R,故sinA>sinB?a>b?A>B,故可得结论.
解答:解:设α,β所对的边分别为a,b三角形外接圆的半径为R,
∵α>β,∴a>b,
∵a=2Rsinα,b=2Rsinβ,∴sinα>sinβ
反之,由正弦定理知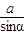 =
=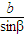 =2R,
=2R,
∵sinα>sinβ,
∴a>b,
∴α>β.
∴“α>β”是“sinα>sinβ”的充要条件.
故选C.
点评:本题以三角形为载体,考查命题充要条件的意义和判断方法,解题的关键是正确运用正弦定理及三角形性质,属基础题,属于基础题.
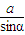 =
=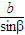 =2R,故sinA>sinB?a>b?A>B,故可得结论.
=2R,故sinA>sinB?a>b?A>B,故可得结论.解答:解:设α,β所对的边分别为a,b三角形外接圆的半径为R,
∵α>β,∴a>b,
∵a=2Rsinα,b=2Rsinβ,∴sinα>sinβ
反之,由正弦定理知
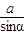 =
=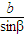 =2R,
=2R,∵sinα>sinβ,
∴a>b,
∴α>β.
∴“α>β”是“sinα>sinβ”的充要条件.
故选C.
点评:本题以三角形为载体,考查命题充要条件的意义和判断方法,解题的关键是正确运用正弦定理及三角形性质,属基础题,属于基础题.

练习册系列答案
相关题目
已知圆的半径为4,a、b、c为该圆的内接三角形的三边,若abc=16
,则三角形的面积为( )
| 2 |
A、2
| ||||
B、8
| ||||
C、
| ||||
D、
|
 已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示.
已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示.