题目内容
已知△ABC是半径为R的圆内接三角形,且2R(sin2A-sin2C)=(
a-b)sinB
(1)求角C;
(2)试求△ABC面积的最大值.
| 2 |
(1)求角C;
(2)试求△ABC面积的最大值.
分析:(1)根据正弦定理,已知等式中的角转换成边,可得a、b、c的平方关系,再利用余弦定理求得cosC的值,可得角C的大小;
(2)根据正弦定理算出c=
R,再由余弦定理c2=a2+b2-2a•bcosC的式子,结合基本不等式找到边ab的范围,利用正弦定理的面积公式加以计算,即可求出△ABC面积的最大值.
(2)根据正弦定理算出c=
| 2 |
解答:解:(1)∵2R(sin2A-sin2C)=(
a-b)sinB,
∴根据正弦定理,得a2-c2=(
a-b)b=
ab-b2,
可得a2+b2-c2=
ab
∴cosC=
=
=
,
∵角C为三角形的内角,∴角C的大小为
(2)由(1)得c=2Rsin
=
R
由余弦定理c2=a2+b2-2a•bcosC,可得
2R2=a2+b2-
a•b≥2ab-
ab=(2-
)ab,当且仅当a=b时等号成立
∴ab≤
=(2+
)R2
∴S△ABC=
absinC≤
•(2+
)R2•
=
R2
即△ABC面积的最大值为
R2
| 2 |
∴根据正弦定理,得a2-c2=(
| 2 |
| 2 |
可得a2+b2-c2=
| 2 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2ab |
| ||
| 2 |
∵角C为三角形的内角,∴角C的大小为
| π |
| 4 |
(2)由(1)得c=2Rsin
| π |
| 4 |
| 2 |
由余弦定理c2=a2+b2-2a•bcosC,可得
2R2=a2+b2-
| 2 |
| 2 |
| 2 |
∴ab≤
| 2R2 | ||
2-
|
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
1+
| ||
| 2 |
即△ABC面积的最大值为
1+
| ||
| 2 |
点评:本题给出三角形的外接圆半径为R,在已知角的关系式情况下,求三角形面积最大值.着重考查了三角形的外接圆、正余弦定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
相关题目
 (2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
(2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
 如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan
如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,又DC⊥面ABC,四边形ACDE为梯形,DE∥AC,且AC=2DE,DC=2,二面角B-DE-C的大小为θ,tan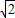 a-b)sinB
a-b)sinB