题目内容
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为
cr、
ar、
br,由S=
cr+
ar+
br得r=
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| a+b+c |
| 3V |
| A+B+C+D |
| 3V |
| A+B+C+D |
分析:由三角形的面积公式可知,是利用等积法推导的,即三个小三角形的面积之和等于大三角形ABC的面积,根据类比推理可知,将四面体分解为四个小锥体,则四个小锥体的条件之和为四面体的体积,由此单调内切球的半径.
解答:解:由条件可知,三角形的面积公式是利用的等积法来计算的.
∴根据类比可以得到,将四面体分解为四个小锥体,每个小锥体的高为内切球的半径,
∴根据体积相等可得
(A+B+C+D)R=V,
即内切球的半径R=
.
故答案为:
.
∴根据类比可以得到,将四面体分解为四个小锥体,每个小锥体的高为内切球的半径,
∴根据体积相等可得
| 1 |
| 3 |
即内切球的半径R=
| 3V |
| A+B+C+D |
故答案为:
| 3V |
| A+B+C+D |
点评:本题主要考查类比推理的应用,要求正确理解类比的关系,本题的两个结论实质是利用了面积相等和体积相等来推导的.

练习册系列答案
相关题目
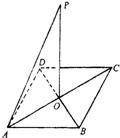 已知边长分别为a米和b米的矩形球场ABCD,在球场正中的上方悬挂一照明灯P,已知球场上各点照明亮度与灯光照射到这点光线和地面夹角的正弦成正比,与这点到灯的距离的平方成反比,若要使球场最边缘的点A获得最好的照明亮度,灯距地面的高度应为多少米?
已知边长分别为a米和b米的矩形球场ABCD,在球场正中的上方悬挂一照明灯P,已知球场上各点照明亮度与灯光照射到这点光线和地面夹角的正弦成正比,与这点到灯的距离的平方成反比,若要使球场最边缘的点A获得最好的照明亮度,灯距地面的高度应为多少米?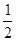 cr、
cr、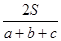 ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.