题目内容
1.给出下列五个命题:①设点M(-1,2)不在直线l:Ax+By+C=0(AB≠0)上,则过点M且与l平行的直线方程是A(x+1)+B(y-2)=0;
②对于任意实数k,直线(k+2)x-(1+k)y-2=0与点(-2,-2)的距离为d,则d的取值范围是$[0,4\sqrt{2}]$;
③设A(0,3)、B(4,5),点P在x轴上,则|PA|+|PB|的最小值是4$\sqrt{5}$;
④已知点P(-3,3)是圆C:(x+2)2+(y-1)2=1外一点,则经过点P的圆的切线方程是3x+4y-3=0
以上命题中正确的序号是①②③.
分析 求出过点M且与l平行的直线方程,可判断①;求出直线(k+2)x-(1+k)y-2=0与点(-2,-2)的距离d的范围,可判断②;求出|PA|+|PB|的最小值,可判断③;求出经过点P的圆的切线方程,可判断④.
解答 解:①设点M(-1,2)不在直线l:Ax+By+C=0(AB≠0)上,则过点M且与l平行的直线方程是:y-2=-$\frac{A}{B}$(x+1),即A(x+1)+B(y-2)=0,故①正确;
②对于任意实数k,直线(k+2)x-(1+k)y-2=0恒过(2,2)点,当直线与y=x垂直时,d取最大值4$\sqrt{2}$,当直线过(-2,2)时,d取最小值0,故d的取值范围是$[0,4\sqrt{2}]$,故②正确;
③设A(0,3)、B(4,5),点P在x轴上,则|PA|+|PB|的最小值是A关于x轴的对称点(0,-3)到(4,5)点的距离d=4$\sqrt{5}$,故③正确;
④已知点P(-3,3)是圆C:(x+2)2+(y-1)2=1外一点,则经过点P的圆的切线方程是3x+4y-3=0或x=-3,故④错误;
故正确的命题为:①②③,
故答案为:①②③
点评 本题以命题的真假判断为载体,考查了直线方程,点到直线距离,两点之间距离,直线与圆的位置关系等知识点,难度中档.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.已知全集I=R,集合A={x|y=$\sqrt{1-x}$},集合B={x|0≤x≤2},则(∁IA)∪B等于( )
| A. | [1,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | (0,+∞) |
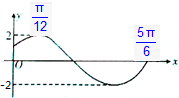 如图是f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象,求函数f(x)的解析式.
如图是f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象,求函数f(x)的解析式.