题目内容
(本小题满分12分)张师傅驾车从公司开往火车站,途径4个交通岗,这4个交通岗将公司到火车站分成5个时段,每个时段的驾车时间都是3分钟,如果遇到红灯要停留1分钟。假设他在各交通岗遇到红灯是相互独立的,并且概率都是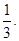
(1)求张师傅此行程时间不小于16分钟的概率;
(2)记张师傅此行程所需时间为Y分钟,求Y的分布列和均值。
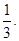
(1)求张师傅此行程时间不小于16分钟的概率;
(2)记张师傅此行程所需时间为Y分钟,求Y的分布列和均值。
解:
(Ⅰ)如果不遇到红灯,全程需要15分钟,否则至少需要16分钟.
张师傅此行程时间不小于16分钟的概率
P=1-(1-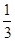 )4=
)4= . …4分
. …4分
(Ⅱ)设此行程遇到红灯的次数为X,则X~B(4,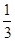 ),
),
P(X=k)=C(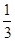 )k(
)k(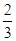 )4-k,k=0,1,2,3,4.
)4-k,k=0,1,2,3,4.
依题意,Y=15+X,则Y的分布列为
Y的均值E(Y)=E(X+15)=E(X)+15=4×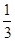 +15=
+15=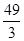 . …12分
. …12分
(Ⅰ)如果不遇到红灯,全程需要15分钟,否则至少需要16分钟.
张师傅此行程时间不小于16分钟的概率
P=1-(1-
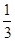 )4=
)4= . …4分
. …4分(Ⅱ)设此行程遇到红灯的次数为X,则X~B(4,
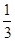 ),
),P(X=k)=C(
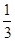 )k(
)k(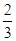 )4-k,k=0,1,2,3,4.
)4-k,k=0,1,2,3,4.依题意,Y=15+X,则Y的分布列为
| Y | 15 | 16 | 17 | 18 | 19 | |
| P | 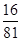 | 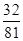 | 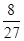 | 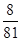 | 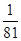 | …10分 |
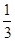 +15=
+15=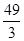 . …12分
. …12分本题考查对立事件的概率和二项分布问题,考查学生的阅读能力和分析能力,第一问采用对立事件的概率求解较为简单,第二问分析得到事件为二项分布是解题的关键。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
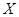 ,求
,求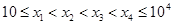 ,
,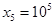 . 随机变量
. 随机变量 取值
取值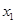 、
、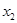 、
、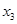 、
、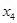 、
、 的概率均为0.2,随机变量
的概率均为0.2,随机变量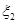 取值
取值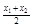 、
、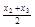 、
、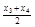 、
、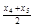 、
、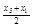 的概率也为0.2.
的概率也为0.2. 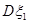 、
、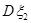 分别为
分别为 .
. ,试写出
,试写出 为小球编号与盒子编号不一致的数目,则
为小球编号与盒子编号不一致的数目,则 表示销售一套该户型住房的利润。
表示销售一套该户型住房的利润。 .
. .
. 服从正态分布
服从正态分布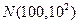 . 已知
. 已知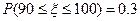 ,估计该班数学成绩在110分以上的人数为______________.
,估计该班数学成绩在110分以上的人数为______________.