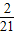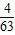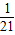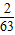题目内容
将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值
,称这些比值中的最小值为这个数表的“特征值”.
(1)当n=2时,试写出排成的各个数表中所有可能的不同“特征值”;
(2)若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=
请分别写出n=3,4,5时数表的“特征值”,并由此归纳此类数表的“特征值”(不必证明);
(3)对于由正整数1,2,3,4,…,n2排成的n行n列的任意数表,若某行(或列)中,存在两个数属于集合{n2-n+1,n2-n+2,…,n2},记其“特征值”为λ,求证:λ≤
.
| a |
| b |
(1)当n=2时,试写出排成的各个数表中所有可能的不同“特征值”;
(2)若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=
|
(3)对于由正整数1,2,3,4,…,n2排成的n行n列的任意数表,若某行(或列)中,存在两个数属于集合{n2-n+1,n2-n+2,…,n2},记其“特征值”为λ,求证:λ≤
| n+1 |
| n |
分析:(1)可设1在第一行第一列,考虑与1同行或同列的两个数的可能,可得特征值;
(2)分别写出当n=3,n=4,n=5时的图表,由特征值的定义可得答案.
(3)设a,b(a>b)为该行(或列)中最大的两个数,易得λ≤
≤
,作差可证
<
,进而可得答案.
(2)分别写出当n=3,n=4,n=5时的图表,由特征值的定义可得答案.
(3)设a,b(a>b)为该行(或列)中最大的两个数,易得λ≤
| a |
| b |
| n2 |
| n2-n+1 |
| n2 |
| n2-n+1 |
| n+1 |
| n |
解答:证明:(1)显然,交换任何两行或两列,特征值不变.
可设1在第一行第一列,考虑与1同行或同列的两个数只有三种可能,2,3或2,4或3,4.
得到数表的不同是
或
…(3分)
(2)当n=3时,数表为此时,数表的“特征值”为
…(4分)
当n=4时,数表为此时,数表的“特征值”为
.…(5分)
当n=5时,数表为此时,数表的“特征值”为
.…(6分)
猜想“特征值”为
.…(7分)
(3)设a,b(a>b)为该行(或列)中最大的两个数,则λ≤
≤
,
因为
-
=
=-
<0
所以
<
,从而λ<
…(13分)
可设1在第一行第一列,考虑与1同行或同列的两个数只有三种可能,2,3或2,4或3,4.
得到数表的不同是
| 3 |
| 2 |
| 4 |
| 3 |
| 7 | 1 | 4 |
| 5 | 8 | 2 |
| 3 | 6 | 9 |
| 4 |
| 3 |
| 13 | 1 | 5 | 9 |
| 10 | 14 | 2 | 6 |
| 7 | 11 | 15 | 3 |
| 4 | 8 | 12 | 16 |
| 5 |
| 4 |
| 21 | 1 | 6 | 11 | 16 |
| 17 | 22 | 2 | 7 | 12 |
| 13 | 18 | 23 | 3 | 8 |
| 9 | 14 | 19 | 24 | 4 |
| 5 | 10 | 15 | 20 | 25 |
| 6 |
| 5 |
猜想“特征值”为
| n+1 |
| n |
(3)设a,b(a>b)为该行(或列)中最大的两个数,则λ≤
| a |
| b |
| n2 |
| n2-n+1 |
因为
| n2 |
| n2-n+1 |
| n+1 |
| n |
| n3-(n3+1) |
| n(n2-n+1) |
| 1 |
| n(n2-n+1) |
所以
| n2 |
| n2-n+1 |
| n+1 |
| n |
| n+1 |
| n |
点评:本题考查类比推理和归纳推理,属基础题.

练习册系列答案
相关题目