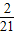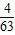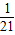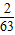题目内容
将正整数1,2,3,…,n…按第k组含k个数的规则分组,则2008在第分析:注意观察,每组数的最后一个数是自然数的和.算得:前62项和为=1953,前63项和为=2016,故2008在第63组内.
解答:解:注意观察,每组数的最后一个数是自然数的和.
1在第1组末,是1的和;
3在第2组末,是1+2的和;
6在第3组末,是1+2+3的和;
…
自然数前n项和求和公式为:S=
,
算得:前62项和为=1953,前63项和为=2016,
所以:
第62组末,是1+2+3+…+62的和,最后一项为1953;
第63组末,是1+2+3+…+63的和,最后一项为2016;
故2008在第63组内.
故答案:63.
1在第1组末,是1的和;
3在第2组末,是1+2的和;
6在第3组末,是1+2+3的和;
…
自然数前n项和求和公式为:S=
| n(n+1) |
| 2 |
算得:前62项和为=1953,前63项和为=2016,
所以:
第62组末,是1+2+3+…+62的和,最后一项为1953;
第63组末,是1+2+3+…+63的和,最后一项为2016;
故2008在第63组内.
故答案:63.
点评:本题考查数列的应用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目