题目内容
(2007
北京海淀模拟)如图所示,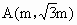 ,
, 两点分别在射线OS、OT上移动,且
两点分别在射线OS、OT上移动,且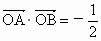 ,O为坐标原点,动点P满足
,O为坐标原点,动点P满足 .
.
(1)
求m·n的值;(2)
求点P的轨迹C的方程,并说明它表示怎样的曲线;(3)
若直线l过点E(2,0)交(2)中曲线C于M、N两点(M、N、E三点互不相同),且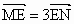 ,求l的方程.
,求l的方程.

答案:略
解析:
解析:
|
解析: (1)由已知得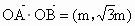 . .
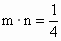 . .
(2) 设P点坐标为(x,y)(x>0),由  得 得
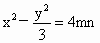 ,又因 ,又因 , ,
∴ P点的轨迹方程为 , ,
它表示以坐标原点为中心,焦点在 x轴上,且实轴长为2,焦距为4的双曲线 的右支. 的右支.
(3) 设直线l的方程为x=ty+2,将其代入C的方程得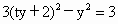 , ,
即  . .
易知 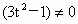 (否则,直线l的斜率为 (否则,直线l的斜率为 .它与渐近线平行,不符合题意). .它与渐近线平行,不符合题意).
设  , ,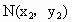 , ,
则 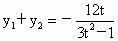 , , . .
∵ l与C的两个交点M,N在y轴的右侧,
又由  ,同理可得 ,同理可得 . .
由  得 得
由  , ,
得  . .
由 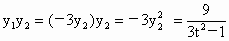 . .
得 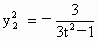 . .
消去  ,得 ,得 . .
解之得  ,满足 ,满足 . .
故所求直线 l存在,其方程为 或 或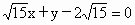 . . |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
(2007
北京海淀模拟)某台机器上安装甲乙两个元件,这两个元件的使用寿命互不影响,已知甲元件的使用寿命超过1年的概率为0.6,要使两个元件中至少有一个的使用寿命超过1年的概率至少为0.9,则乙元件的使用寿命超过1年的概率至少为[
]|
A .0.3 |
B .0.6 |
C .0.75 |
D .0.9 |
(2007
北京海淀模拟)设m、n是不同的直线,α、β、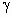 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①
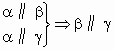 ②
②
②
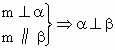 ④
④
其中为真命题的是
[
]|
A .①④ |
B .②③ |
C .①③ |
D .②④ |
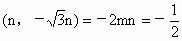



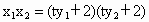
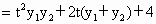
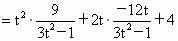




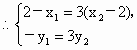
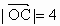 ,
, ,动点M到直线AB的距离是它到点D的距离的2倍.
,动点M到直线AB的距离是它到点D的距离的2倍.
 ,动点P满足
,动点P满足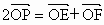 ,求直线KP的斜率的取值范围.
,求直线KP的斜率的取值范围.
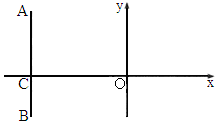
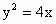 及椭圆
及椭圆 的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是
的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是
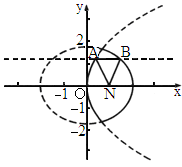



 为数列
为数列 的前n项和,且
的前n项和,且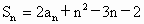 ,n=1,2,3,….
,n=1,2,3,….
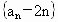 为等比数列;
为等比数列;
 ,求数列
,求数列 的前n项和
的前n项和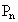 ;
;
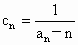 ,数列
,数列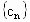 的前n项和为
的前n项和为 ,
,
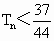 .
.