题目内容
已知在△ABC中,内角A,B,C所对的边分别为a,b,c,且acos C+ c=b.
c=b.
(1)求角A;
(2)若a=1,且 c-2b=1,求角B.
c-2b=1,求角B.
(1)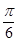 (2)
(2)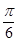
解析

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
已知在△ABC中,内角A,B,C所对的边分别为a,b,c,且acos C+ c=b.
c=b.
(1)求角A;
(2)若a=1,且 c-2b=1,求角B.
c-2b=1,求角B.
(1)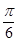 (2)
(2)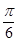
解析

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案