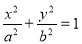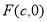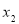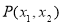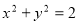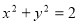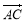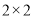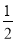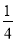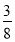题目内容
已知定点A(-2,0)和B(2,0),曲线E上任一点P满足|PA|-|PB|=2.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤ ),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
(1)x2-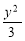 =1(x>0) ;(2)|PQ|min=6;(3) a≤-1.
=1(x>0) ;(2)|PQ|min=6;(3) a≤-1.
【解析】
试题分析:(1)由题意可知P点轨迹为双曲线,由a,c求出b的值,则方程可求;
(2)当直线斜率存在时,设出直线方程,和双曲线方程联立后求得判别式大于0,再由两根之和大于0,且两根之积大于0联立求得k的范围由弦长公式写出弦长,借助于k的范围求弦长的范围,当斜率不存在时直接求解;
(3)由题意,|CR|=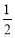 |PQ|。若直线PQ不垂直于x轴,由|CR|=
|PQ|。若直线PQ不垂直于x轴,由|CR|= -a=
-a=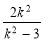 -a
-a
∴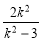 -a=
-a=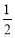 ·
·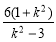 ,a=
,a=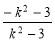 =-1+
=-1+ <-1,若直线PQ垂直于x轴,这时|PQ|=6,|CR|=2-a ∴a=-1, 综上a≤-1.
<-1,若直线PQ垂直于x轴,这时|PQ|=6,|CR|=2-a ∴a=-1, 综上a≤-1.
试题解析:【解析】
(1)由双曲线的定义得:曲线E是以A, B为焦点的双曲线的右支,所以曲线E的方程为:x2-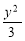 =1(x>0) 2分
=1(x>0) 2分
(2)若直线PQ不垂直于x轴,设直线PQ的方程为:y=k(x-2)
由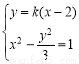 ,得(3-k2)x2+4k2x-(4k2+3)=0 3分
,得(3-k2)x2+4k2x-(4k2+3)=0 3分
设p(x1,y1),Q(x2,y2),这里x1>0,x2>0
则: 得:k2>3 6分
得:k2>3 6分
|PQ|= |x1-x2|=
|x1-x2|=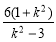 =6+
=6+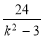 >6 6分
>6 6分
若直线PQ垂直于x轴,则直线PQ的方程为x=2。 8分
这时P(2,3),Q(2,-3),所以|PQ|=6,
综上:|PQ|min=6 9分
(3)据题意得:|CR|=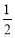 |PQ|。若直线PQ不垂直于x轴,
|PQ|。若直线PQ不垂直于x轴,
由|CR|= -a=
-a=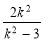 -a 10分
-a 10分
∴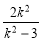 -a=
-a=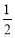 ·
·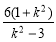 ,a=
,a=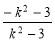 =-1+
=-1+ <-1 12分
<-1 12分
若直线PQ垂直于x轴,这时|PQ|=6,|CR|=2-a
∴a=-1. 13分
综上a≤-1. 14分
考点:直线与圆锥曲线的关系.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案