题目内容
【题目】已知点
,点
是圆
上的任意一点,，线段
的垂直平分线与直线
交于点
.
（1）求
点的轨迹方程；
（2）若直线
与点
的轨迹相切，且与圆
相交于点
和
，求直线
和三角形
的面积．
【答案】(1) 
；（2）
.
【解析】试题分析：（1）根据已知，由平面几何知识可得
，所以E的轨迹是以点A,C为焦点的椭圆，从而可得轨迹方程；（2）由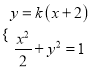
，
得
，根据判别式为零可得直线斜率，从而可得直线方程，再利用点到直线距离公式与三角形面积公式可得结果.
试题解析：（1）由题意可知
E的轨迹是以点A,C为焦点的椭圆
所以椭圆的方程
.
(2)由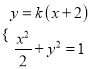
，
得
又
与点
的轨迹相切
即
， 又
，所以
， 
的方程
圆心C到
的距离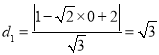
由垂径定理可知， 
又
原点O到直线
的距离
.
【方法点晴】本题主要考查定义法求轨迹方程、点到直线的距离公式及三角形面积公式，属于难题.求轨迹方程的常见方法有:①直接法，设出动点的坐标
，根据题意列出关于
的等式即可；②定义法，根据题意动点符合已知曲线的定义，直接求出方程；③参数法，把
分别用第三个变量表示，消去参数即可；④逆代法，将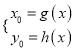
代入
.本题（1）就是利用方法②求得
的轨迹方程的.
【题目】某畜牧站为了考查某种新型药物预防动物疾病的效果，利用小白鼠进行试验，得到如下丢失数据的
列联表
患病 | 未患病 | 总计 | |
没服用药 | 20 | 30 | 50 |
服用药 |
|
| 50 |
总计 |
|
| 100 |
设从没服用药的小白鼠中任取两只，未患病的动物数为
，从服用药物的小白鼠中任取两只，未患病的动物数为
，得到如下比例关系：
（1）求出列联表中数据
，
，
，
的值
（2）是否有
的把握认为药物有效？并说明理由
（参考公式：
，当
时，有
的把握认为A与B有关；
时，有的把握认为A与B有关．
【题目】已知函数f（x）=x2﹣2|x﹣a|（a∈R）．
（1）若函数f（x）为偶函数，求a的值；
（2）当a＞0时，若对任意的x∈[0，+∞），不等式f（x﹣1）≤2f（x）恒成立，求实数a的取值范围．
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关，现从该市“五一”出游旅客中随机抽取500人进行调查，得到如下2×2列联表：（单位：人）
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
（Ⅰ）据此样本，有多大的把握认为选择“有水的地方”与性别有关；
（Ⅱ）若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况，现从该市的全体出游旅客（人数众多）中随机抽取3人，设3人中选择“有水的地方”的人数为随机变量X，求随机变量X的数学期望和方差．
附临界值表及参考公式：
P（K2≥k0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
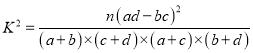，n＝a＋b＋c＋d．
