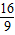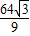Question

表面积为16π的球的内接正方体的体积为（　　）

• A、8
• B、

  16

  9

• C、

  64 3

  9

• D、16

Answer 1

分析：求出球的半径，正方体的对角线是外接球的直径，然后求出想正方体的棱长，即可求出正方体的体积．

解答：解：表面积为16π的球的半径为：4πr²=16π，r=2，
正方体的对角线为：4；正方体的棱长为：

4

3

，
正方体的体积为：(

4

3

)3=

64 3

9

，
故选C．

点评：本题是基础题，考查球的内接正方体的体积的求法，正方体的对角线就是外接球的直径，是解题的关键，考查计算能力．