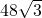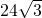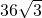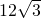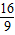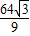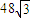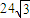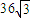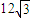Question

表面积为16π的球内切于正三棱柱ABC-A₁B₁C₁的各个面，则该项棱柱的体积为（　　）

• A、48

  3

• B、24

  3

• C、36

  3

• D、12

  3

Answer 1

分析：由题意根据题中条件：“球内切于正三棱柱ABC-A₁B₁C₁的各个面”求出正三棱柱的高、底面边长、底面高，即可求出正三棱柱的体积．

解答：解：设球半径为R，
由题意，正三棱柱的高是直径为2R，正三棱柱底面正三角形的内切圆的半径是R，
所以正三角形的边长是2

3

R，高是3R，则正三棱柱的体积为V=

1

2

•2

3

R•3R•2R=6

3

R³．
由于表面积为16π的球，∴R=2．
则该项棱柱的体积为：48

3

．
故选A．

点评：本题是基础题，考查正三棱柱的内切球与正三棱柱的关系，通过二者的关系求出正三棱柱的体积，考查计算能力，逻辑推理能力．