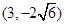题目内容
求满足下列条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过两点P(
,
),Q(0,-
);
(2)经过点(2,-3)且与椭圆9x2+4y2=36具有共同的焦点.
(1)焦点在坐标轴上,且经过两点P(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
(2)经过点(2,-3)且与椭圆9x2+4y2=36具有共同的焦点.
分析:(1)解法1:利用待定系数法,分类讨论,解方程组,可求椭圆的标准方程;
解法2:设所求椭圆的标准方程为mx2+ny2=1(m>0,n>0,m≠n),解方程组,可求椭圆的标准方程;
(2)设出与椭圆9x2+4y2=36具有共同的焦点的椭圆方程,将(2,-3)代入,即可求得椭圆的标准方程.
解法2:设所求椭圆的标准方程为mx2+ny2=1(m>0,n>0,m≠n),解方程组,可求椭圆的标准方程;
(2)设出与椭圆9x2+4y2=36具有共同的焦点的椭圆方程,将(2,-3)代入,即可求得椭圆的标准方程.
解答:解:(1)解法1:①当所求椭圆的焦点在x轴上时,设它的标准方程为
+
=1(a>b>0),依题意应有
,解得
,因为a>b从而方程组无解;
②当所求椭圆的焦点在y轴上时,设它的标准方程为
+
=1(a>b>0),依题意应有
,解得
,所以所求椭圆的标准方程为
+
=1.
故所求椭圆的标准方程为
+
=1.
解法2:设所求椭圆的标准方程为mx2+ny2=1(m>0,n>0,m≠n),依题意得
,解得
,从而所求椭圆的标准方程为
+
=1.
(2)∵椭圆9x2+4y2=36的焦点坐标为(0,±
),从而可设所求椭圆的方程为
+
=1(λ>0),
又∵经过点(2,-3),从而得
+
=1,解得λ=10或λ=-2(舍去),
故所求椭圆的标准方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
|
|
②当所求椭圆的焦点在y轴上时,设它的标准方程为
| y2 |
| a2 |
| x2 |
| b2 |
|
|
| y2 | ||
|
| x2 | ||
|
故所求椭圆的标准方程为
| y2 | ||
|
| x2 | ||
|
解法2:设所求椭圆的标准方程为mx2+ny2=1(m>0,n>0,m≠n),依题意得
|
|
| y2 | ||
|
| x2 | ||
|
(2)∵椭圆9x2+4y2=36的焦点坐标为(0,±
| 5 |
| x2 |
| λ |
| y2 |
| λ+5 |
又∵经过点(2,-3),从而得
| 4 |
| λ |
| 9 |
| λ+5 |
故所求椭圆的标准方程为
| x2 |
| 10 |
| y2 |
| 15 |
点评:本题考查椭圆的标准方程,考查待定系数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
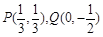 ;
;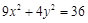 具有共同的焦点.
具有共同的焦点.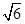 ),Q(
),Q(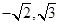 ). (2)焦点在x轴上,焦距为4,并且过点
). (2)焦点在x轴上,焦距为4,并且过点